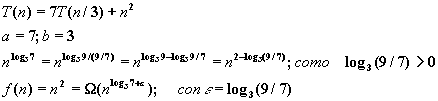
Tiempo: 105 Minutos (de 8:00 a 9:45)
1.- Encuentre el valor asintótico para la recurrencia: T(n) = 7T(n/3) + n2
Justifique su respuesta.
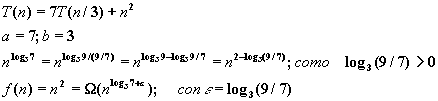
Posible caso 3, debemos verificar:
![]()
Luego se cumplen las condiciones del caso 3 y se tiene: ![]() .
.
2.- Mínimo y máximo entre n elementos.
a) Encuentre el menor número de comparaciones necesarias para encontrar el mínimo entre n elementos.
b) Encuentre un algoritmo (codifique en C, C++, o pseudo-lenguage) que encuentre el máximo y mínimo de entre n elementos con no más de 3*é n/2ù comparaciones.
a) El mínimo lo podemos obtener asumiendo inicialmente el primer elemento como el mínimo y luego comparando sucesivamente éste con cada uno de los restantes. EN cada caso el mínimo se actualiza si el número comparado es menor. Se desprende entonces que el número de comparaciones es n-1.
b) Código:
int MinMax(int A[], int n, int &min, int &max) {
if (n<0) return -1; /* no hay mínimo ni máximo */
if (n%2==0){ /* n es par */
if (A[n/2-1] < A[n/2]) {
min = A[n/2-1]; max= A[n/2];
} else {
min=A[n/2]; max = A[n/2-1];
}
}else {
min=max=A[n/2]; /* n es impar */
}
for ( i = 0; i < (n-1)/2; i++) {
if (A[i] < A[n-1-i]) {
if (A[i] < min) min=A[i];
if (max <A[n-1-i]) max =A[n-1-i];
} else {
if (A[n-1-i] < min) min=A[n-1-i];
if (max <A[i]) max =A[i];
}
return 1;
}
La idea es efectuar comparaciones de a dos elementos por vez. Luego se compara el menor de ambos con el mínimo hasta el momento y el mayor con el máximo hasta el momento. De este modo con tres comparaciones en que participan los datos se procesan dos datos de entrada. Como resultado de obtiene é n/2ù etapas de procesamiento en la que efectuamos tres comparaciones, en total 3*é n/2ù comparaciones.
3.- Muestre los pasos seguidos por Quicksort para ordenar la siguiente secuencia.
<u, n, e, j, e, m, p, l, o, d, e, o, r, d, e, n>
<n, n, e, j, e, m, p, l, o, d, e, o, r, d, e> <u>
<e, d, e, j, e, m, e, l, d> <o, p, o, r, n, n> <u>
<d, d, e, e> <j, m, e, l, e> <n, n, o> <r, p, o> <u>
<d> <d, e, e> <e, e> <m, l, j> <n> <n, o> <o, p> <r> <u>
<d> <d> <e, e> <e> <j, l> <m> <n> <n> <o> <o> <p> <r> <u>
<d> <d> <e> <e> <e> <e> <j> < l> <m> <n> <n> <o> <o> <p> <r> <u>
4.- Escriba una función en C o C++ que dado un arreglo de n notas de un certamen USM retorne la k-ésima mejor nota. Ojo la primera mejor nota es LA mejor nota, la segunda mejor nota es la siguiente inmediatamente inferior, y así sucesivamente.
int K_esima_mejor(int notas[], int n, int k) {
k= n-(k-1);
int C[101], i, j;
for ( i=0; i < 101; i++)
C[i]=0;
for (j=0; j < n; j++)
C[nota[j]]++;
for (i=1; i<101; i++)
C[i]+=C[i-1];
for (i=100; i>0; i--)
if (C[i] >= k)
return i;
}
5.- Dada una lista circular L doblemente enlazada. Desarrolle una función que dado dos punteros x, y a nodos de la lista L, permita intercambiarlos.
typedef struct _nodo {
struct _nodo * next, * prev;
Elemento elemento;
} NODO;
void swap (NODO *x; NODO*y) {
NODO * tmp;
tmp =x->prev;
x->prev = y->prev;
y->prev = tmp;
tmp = x->next;
x->next=y->next;
y->next = tmp;
}
void swap_nodos( NODO * * pL, NODO * x, NODO * y) {
NODO * aux = x;
if (x==y) return;
if (*pL==x) *pl = y;
if (*pl==y) *pl = x;
if (x->next !=y && x->prev != y) {
x->prev->next = y;
x->next->prev=y;
y->prev->next = x;
y->next->prev=x;
swap (x,y);
} else if (x->next == y && x->prev == y)
return;
else if (x->next == y) {
y->next->prev = x;
x->prev->next = y;
swap(x,y);
}else {
x->next ->prev =y;
y->prev->next =x;
}
}
6.- Se desean ingresar 3/4 M elementos a una tabla de hash cerrado inicialmente vacía y con M entradas. ¿Qué es más económico en término de número de operaciones: duplicar el tamaño de la tabla hash cuando se alcance un factor de carga de 0.5 ó triplicar su tamaño cuando el factor de carga llega a 1/3? Incluya su desarrollo.
7.- Haga una función en C o C++ que retorne la altura de un árbol binario.
typdef struct nodo_ {
struct nodo_ *left, *right;
Elemento elemento;
} NODO;
int altura (NODO * T) {
int a, b;
if ( T == NULL)
return 0;
else if (T-> left != NULL || T->right != NULL) {
a = altura (T->left);
b = altura(T->right);
return(a>b?a+1:b+1);
} else return 0;
}
8.- Resolviendo estadísticas de orden en un árbol de búsqueda binaria se tiene:
int OS_Rank(TREE_NODE * T, TREE_NODE * x) {
int r;
TREE_NODE *y;
if (x->left == NULL)
r = 1;
else
r = x->left->size + 1;
y = x;
while (y != T) {
if ( y == y -> p->right )
r = r+y->p->size - y->size; /* línea a cambiar */
y = y->p;
}
return r;
}
Explique si la "línea a cambiar" puede ser sustituida por:
r = r+y->p->left->size +1;
Justifique su respuesta.
No, no puede ser reemplazada. La razón se obtiene de analizar el caso en que el padre de y no posee hijo izquierdo. En este caso la codificación propuesta como alternativa falla al intentar acceder al tamaño del sub-árbol del hijo izquierdo. La codificación original no presenta problemas ya que depende sólo del tamaño del padre de y y de y mismo ambos bien definidos dentro del cuerpo del if.