Tiempo: 105 Minutos (de 10:00 a 11:45)
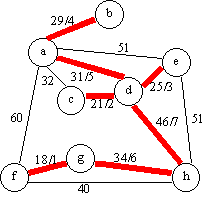
1.- Para el gráfico de la figura 1, muestre una solución obtenida usando el algoritmo de Kruscal para el obtener el árbol de expansión mínima (Minimum spanning tree). Enumere los arcos de su solución según el orden en que fueron incorporados a ésta.
żEs su árbol la única expansión mínima posible?
20 pts

La solución es única.
2.- Para el grafo de la figura l, muestre la solución obtenida usando el algoritmo de Dijkstra para el nodo b. Muestre el orden en que los arcos son incorporados en su solución. (si le complica la nodireccionalidad del grafo, reemplace cada arco por dos arcos direccionales de igual peso al indicado)
żEs su solución la única?
20 pts
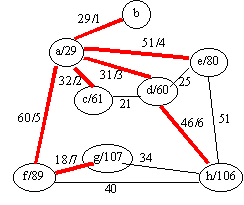
La solución (árbol) es única, claro que hay varios ordenes en que los arcos pudieron ser incorporados.
3.-Sea un grafo G=(V,E). V representa un conjunto de localidades geográficas separadas por puentes y cada arco (u,v) de E el puente entre la localidad u y v. Cada arco tiene asociado un número real c(u,v). Interpretamos c(u,v) como la carga máxima tolerada por el puente. Proponga un algoritmo eficiente para encontrar el camino que soporte mayor carga para moverse entre dos vértices dados.
Primero indique cual es su idea general para resolver el problema. Para su algoritmo use sintaxis similar a la usada en clases; i.e. no debe hacerlo en C.
25 pts
Hay varias formas de solución, vía Bellman-Ford por ejemplo, aquí se presentará la solución usando una adaptación del algoritmo de Dijkstra.
La idea es ir expandiendo el conjunto S de nodos ya alcanzados buscando la ruta cuyo puente más débil sea el mayor de todas las rutas alternativas. Para ello redefinimos el arreglo d , tal que d[v] es la carga del puente más débil de la ruta que nos conduce al vértice v.
Sea s y t los nodos de inicio y término del recorrido pedido. d[s] = ¥ , porque al no atravesar ningún puente desde s a s la carga tolerada en infinita. Todos los otros nodos deben partir con d[v]=0 porque en principio no hay camino, luego la carga tolerada en cero.
La función de relajación debe ser tal que opto por llegar a v través de u siempre que esa ruta me permita llevar más carga; es decir, que Mínimo{d[u], c(u,v)} > d[v]. En cada iteración debo seleccionar el nodo que cuya carga ( que es la mínima para su ruta) sea la mayor entre los nodos. Una vez seleccionado, no hay forma de mejorar la llegada a este nodo a través de vías alternativas por nodos a ser considerados en el futuro ya que ellos tendrán un cuello de botella peor (el puente más débil). Bien así queda entonces el algoritmo:
Relax (u,v, c){
aux = Mínimo{ d[u], c[u,v] }; /* cuello de botella para llegar a v vía u */
if (aux > d[v] ){ /* cuello de botella previo para v era peor */
d[v] = aux;
p[v] = u;
}
}
Ruta_de_Mayor_Carga(G, w, s, t) { /* s nodo inicio, t nodo término */
for (cada vértice v en V[G] ) {
d [v] = 0; /* peor cuello de botella imaginable */
p [v] = NIL;
}
d [s] = ¥
;
S = {}; /* S Contiene el arreglo de los nodos cuyo camino de mayor capacidad (cuello de botella menos crítico) ya ha sido encontrado */
Q = V [G];
while (Q != {}) {
u = Extract_Max(Q);
S = S È
{u};
if ( u == t)
return; /* la ruta ya ha sido encontrada y se puede obtener recorriendo el arreglo p desde t a s */
for ( cada vértice v en adj[u] )
Relax(u,v, w);
}
}
También se pudo resolver usando Prim o Kruskal
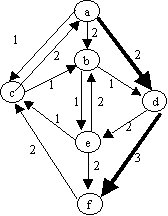
4.- Encuentre el flujo máximo para la red mostrada en Fig2. Muestre los pasos del algoritmo (redes residuales y redes de flujo de cada iteración)
25 pts
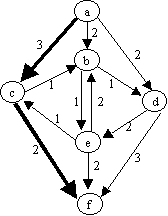
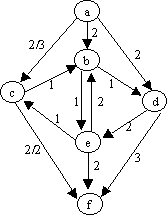
Flujo hasta ahora: 0 + 2
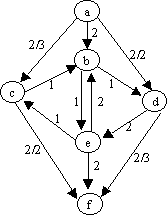
Flujo hasta ahora es: 2 + 2 = 4
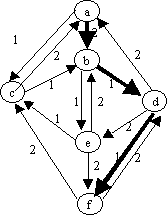
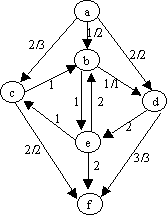
Flujo hasta ahora es: 4 + 1 = 5
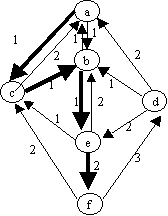
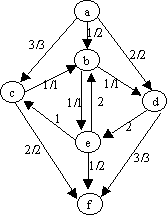
Flujo hasta ahora es: 5 + 1 = 6

No hay camino de aumento posible en la red residual resultante, por lo tanto el flujo máximo de a hacia f es: 6.
5.-
a) De qué tamaño es el clique (o pandilla) de tamaño máxima en el grafo de Fig 1. Muestre un clique.
b) Muestre una cubierta de tamaño mínimo para el grafo de Fig 1.
10 pts
a) Un tamaño máximo para un clique en el grafo de Fig 1 es 3. Un ejemplo es: {a,c,d}.
b) Una cubierta de tamaño mínimo es: {a, d, h, f }. Otra opción sería {a, d, h, g} No hay más cubiertas de tamaño 4.
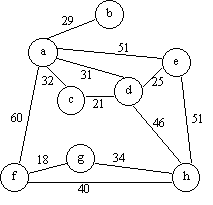

Fig1: Grafo Problema 1,2, 5 Fig2: Red de flujo problema 4