They are the NULL black nodes of property 2.
| Data Structures and Algorithms |
| 8.2 Red-Black Trees |
A red-black tree is a binary search tree with
one extra attribute for each node: the colour,
which is either red or black.
We also need to keep track of the parent of each node,
so that a red-black tree's node structure would
be:
struct t_red_black_node {
enum { red, black } colour;
void *item;
struct t_red_black_node *left,
*right,
*parent;
}
For the purpose of this discussion,
the NULL nodes which terminate the tree are considered to
be the leaves and are coloured black.
|
|
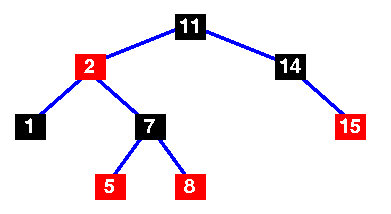
 | A basic red-black tree |
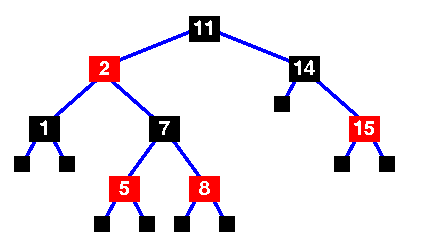
 | Basic red-black tree with the
sentinel nodes added.
Implementations of the red-black tree algorithms will usually include
the sentinel nodes as a convenient means of flagging that you have
reached a leaf node. They are the NULL black nodes of property 2. |
This demonstrates why the red-black tree is a good search tree: it can always be searched in O(log n) time.
As with heaps, additions and deletions from red-black trees destroy the red-black property, so we need to restore it. To do this we need to look at some operations on red-black trees.
|
A rotation is a local operation
in a search tree that preserves
in-order traversal key ordering.
Note that in both trees, an in-order traversal yields:
A x B y C |  |
left_rotate( Tree T, node x ) {
node y;
y = x->right;
/* Turn y's left sub-tree into x's right sub-tree */
x->right = y->left;
if ( y->left != NULL )
y->left->parent = x;
/* y's new parent was x's parent */
y->parent = x->parent;
/* Set the parent to point to y instead of x */
/* First see whether we're at the root */
if ( x->parent == NULL ) T->root = y;
else
if ( x == (x->parent)->left )
/* x was on the left of its parent */
x->parent->left = y;
else
/* x must have been on the right */
x->parent->right = y;
/* Finally, put x on y's left */
y->left = x;
x->parent = y;
}
rb_insert( Tree T, node x ) {
/* Insert in the tree in the usual way */
tree_insert( T, x );
/* Now restore the red-black property */
x->colour = red;
while ( (x != T->root) && (x->parent->colour == red) ) {
if ( x->parent == x->parent->parent->left ) {
/* If x's parent is a left, y is x's right 'uncle' */
y = x->parent->parent->right;
if ( y->colour == red ) {
/* case 1 - change the colours */
x->parent->colour = black;
y->colour = black;
x->parent->parent->colour = red;
/* Move x up the tree */
x = x->parent->parent;
}
else {
/* y is a black node */
if ( x == x->parent->right ) {
/* and x is to the right */
/* case 2 - move x up and rotate */
x = x->parent;
left_rotate( T, x );
}
/* case 3 */
x->parent->colour = black;
x->parent->parent->colour = red;
right_rotate( T, x->parent->parent );
}
}
else {
/* repeat the "if" part with right and left
exchanged */
}
}
/* Colour the root black */
T->root->colour = black;
}
Here's an example of the insertion operation.
|
Red-Black Tree Animation This animation was written by Linda Luo, Mervyn Ng, Anita Lee, John Morris and Woi Ang. |
|
Please email comments to: morris@ee.uwa.edu.au |
Examination of the code reveals only one loop. In that loop, the node at the root of the sub-tree whose red-black property we are trying to restore, x, may be moved up the tree at least one level in each iteration of the loop. Since the tree originally has O(log n) height, there are O(log n) iterations. The tree_insert routine also has O(log n) complexity, so overall the rb_insert routine also has O(log n) complexity.
Key terms |
| Continue on to AVL Trees | Back to the Table of Contents |