Podemos también decir que si el procedimiento para calcular el intervalo de confianza del 95% es usado muchas ocasiones, el 95% de las veces el intervalo contendrá al parámetro.
Intervalos de Confianza pueden ser calculados para cualquier parámetro estimado. Por ejemplo se podría estimar la proporción de personas que podrían pasar un programa de entrenamiento, o se podría estimar el número mínimo de experimentos a realizar para que el valor promedio del fenómeno se encuentre con cierta probabilidad en un rango dado.
En adelante se orienta esta información al estimador del promedio cuando no conocemos la desviación estándar del fenómeno, para la cual se usa un estimador. Otros estimadores son estudiados en HyperStat OnLine.
Intervalo de Confianza para el promedio m usando una desviación estándar estimada
Es muy raro que cuando deseemos estimar el valor medio para una fenómeno ya conozcamos su desviación estándar. Es así que para obtener el intervalo de confianza casi siempre debemos estimar ambos m (mean) y s (standar deviation).
Notación: M es el valor medio calculado para los N datos obtenidos (N es el tamaño de la muestra usando lenguaje estadístico).
Hay tres valores usados en la construcción del intervalo de confianza para m: el promedio para la muestra de datos (M), el valor t que depende del nivel de confianza, y el error estándar del promedio sM=
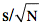 (El error estándar corresponde a la
desviación estándar de la distribución para el valor promedio de las
muestras). El
intervalo de
confianza tiene a M en su centro y se extiende en ambas
direcciones en el producto t*sM , A este valor
se le llama margen de error. Así la fórmula para el intervalo de
confianza para m
cuando s es estimado es:
(El error estándar corresponde a la
desviación estándar de la distribución para el valor promedio de las
muestras). El
intervalo de
confianza tiene a M en su centro y se extiende en ambas
direcciones en el producto t*sM , A este valor
se le llama margen de error. Así la fórmula para el intervalo de
confianza para m
cuando s es estimado es:M - t*sM
m
M + t*sM [1]
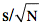 ,
y t depende del nivel de confianza y de los grados de
liberta. s es el valor estimado para la desviación
estándar del fenómeno.
,
y t depende del nivel de confianza y de los grados de
liberta. s es el valor estimado para la desviación
estándar del fenómeno.Grados de libertad: El grado de libertad es el número de términos independientes usados para estimar un parámetro. En general el grado de libertad es igual al número de datos independientes menos el número de parámetros estimados como pasos intermedios en la determinación del parámetro mismo. Por ejemplo, si deseamos estimar la varianza de una muestra de N datos independientes, el grado de libertad es igual al número de datos N menos el número de parámetros estimados como pasos intermedios (uno,m es estimado por M), lo cual es N-1.
Cálculo de los términos del intervalo de confianza:
Promedio y varianza
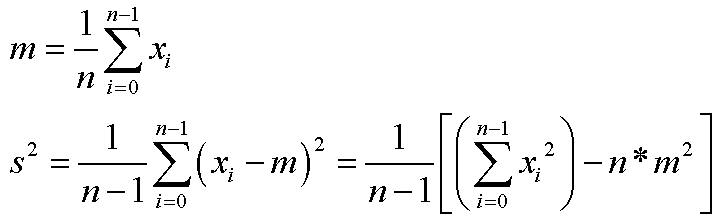
Error estándar del promedio: sM =
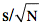 = s / sqrt(N)
= s / sqrt(N)Factor dependiente de nivel de confianza y grados de libertad t: este valor está tabulado. El nivel de confianza normalmente es dado y el grado de libertad es el de sM el cual es igual a N-1.
Ejemplo de Aplicación: Suponga que estamos interesados en estimar la rapidez de lectura promedio (número de palabras por minuto) de estudiantes egresados de cuarto medio y calcular esto con un 95% de nivel de confianza. Para ello tomamos una muestra al azar de 6 graduados y obtuvimos que sus rapideces fueron: 200, 240, 300, 410, 600, y 450.
Para estos datos:
M = 366.67De este modo se obtiene que el intervalo de confianza del 95% es:
sM = 60.97
df = 6 - 1 = 5
t = 2.571
M ± t * sM = 366.67 ± 156.75
Luego 210m
523
Así, podemos decir que con un 95% de certeza que la rapidez
de lectura promedio de los graduados de enseñanza media
está entre 210 y 523 palabras por minuto.
Resumen
1.- Calcular M y s usando
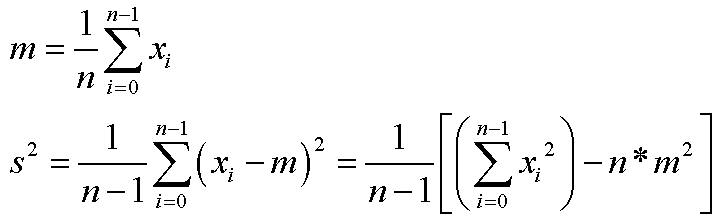
3.- Calcular sM = 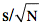 = s /
sqrt(N)
= s /
sqrt(N)
4.- Calcular df = N-1
5.- Encontrar t para estos grados de libertad usando la tabla para t
6.- El intervalo de confianza pasa a ser: M ± t* sM
Suposiciones
1.- La distribución de los datos es normal.
2.- Los satos son obtenidos en forma aleatoria y son independientes.