Ejercicios para el 3º Certamen
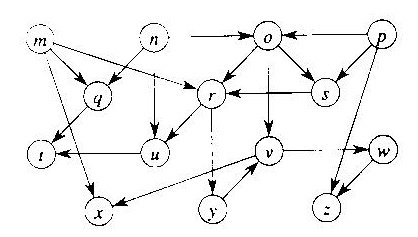
1.- Obtener las componenetes fuertemente conexas para el grafo de la figura.

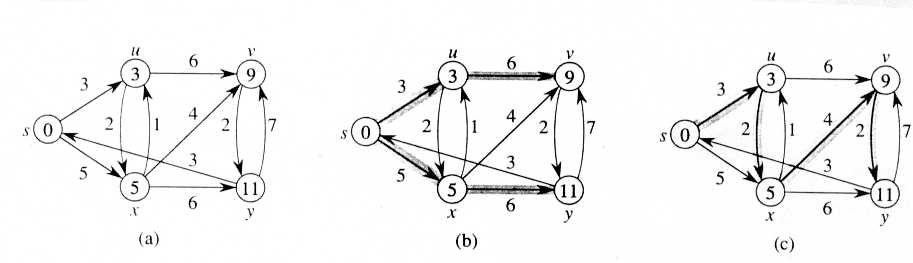
3.- Corra el algoritmo de Dijkstra sobre el grafo dirigido de la figura, primero usando el vertice s como fuente y luego usando el vertice y como fuente. Muestre los valores de d, p y S despues del lazo while.
4.- Invente un ejemplo simple de un grafo dirigido con arcos de peso negativo para el cual el algoritmo de Dijkstra produzca una respuesta incorrecta.
5.- Suponga que cambiamos la condición del while en el algoritmo
de Dijkstra a lo siguiente: while (|Q| > 1)
Esto causa que el loop while se ejecute |V|-1 veces en lugar de |V|.
¿Se obtiene así un algoritmo correcto?
6.- Sea un grafo G=(V,E) sobre el cual cada arco (u,v) en E tiene asociado un valor r(u,v), el cual es un número real en el rango 0<= r(u,v) <=1 que representa la confiabilidad de un canal de comunicación desde el vertice u al v. Interpretamos r(u,v) como la probabilidad que el canal desde u a v no fallará, y suponemos que estas probabilidades son independientes. Proponda un algoritmo eficiente para encontrar el camino más confiable entre dos vértices dados.
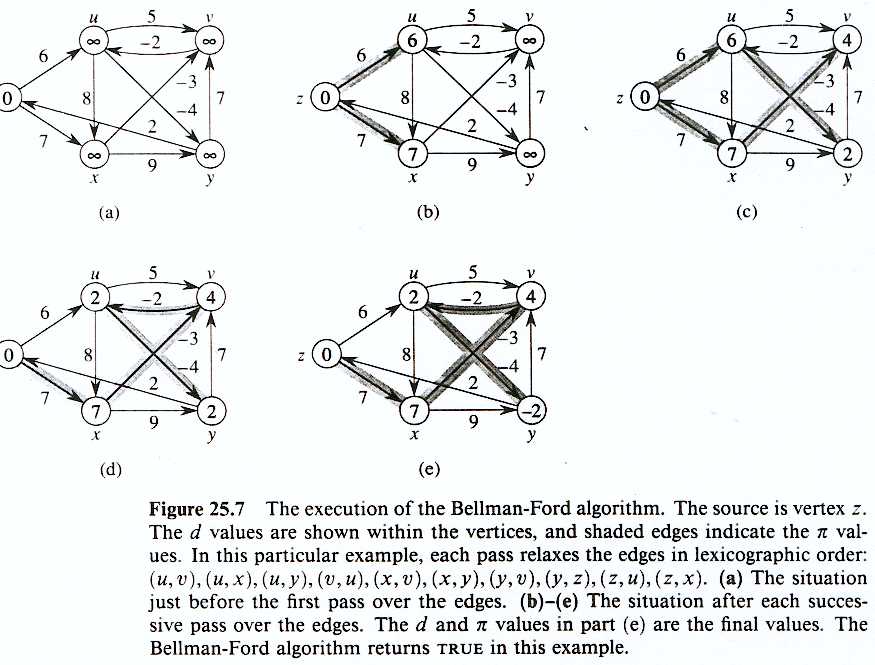
7.- Para el grafo de la figura corra el algoritmo Bellman-Ford usando el vértice "y" como fuente u origen. "Relaje" los arcos en orden alfabético en cada pasada (Por ejemplo (u,v) va primero que (u,x) y luego de considerar los arcos con origen en u, debo cosiderar los arcos on origen en v. Luego de cada pasada por todos los arcos muestre los arreglos d y p. Finalmente, cambie el peso del arco (y,v) a 4 y corra el algoritmo nuevamente usando z como fuente.