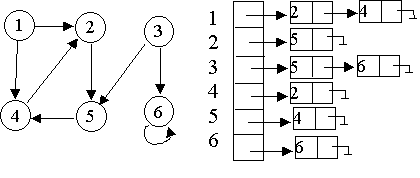
1.-Muestre el resultado de correr el algoritmo de busqueda en profundidad sobre el grafo dirigido adjunto. Use el vertice 3 como fuente.

2.- Encuentre un algoritmo eficiente para determinar si un grafo dirigido contiene o no ciclos.

3.-Encuentre las componentes fuertemente conexas del grafo del problema 1. Muestre el grafo con los tiempos de terminos obtenidos, luego muestre el grafo con los arcos invertidos, y finalnete las componentes fuiertemente conexas.

4.- Para el siguiente grafo muestre los pasos seguido spor el algoritmo de PRIM y KRUSKAL.

5.- M uestre el resultado del algoritmo de Dijkstra para el nodo d del grafo del ejercicio 4.

6.- Sea un grafo G=(V,E) sobre el cual cada arco (u,v) en E tiene asociado un valor r(u,v), número real en el rango 0<= r(u,v) <=1 que representa la confiabilidad de un canal de comunicación desde el vertice u al v. Interpretamos r(u,v) como la probabilidad que el canal desde u a v no fallará, y suponemos que estas probabilidades son independientes. Proponda un algoritmo eficiente para encontrar el camino más confiable entre dos vértices dados.

7.- Encontrar la asociación bipartita máxima para el grafo de la figura.

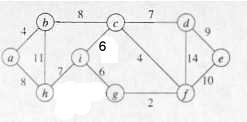
8.- Se tiene puntos conectados en red con enlacen de capacidad según se muestra en la figura. Determine cual es el máximo teórico de trafico que se puede transferir desde el nodo a hacia el nodo g. Asuma que los enlaces son bidireccionales y la capacidad indicada es la de cada dirección.

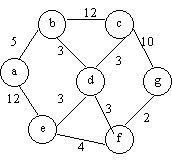
9.- Para el grafo del problema previo:

a) Encontrar un Clique (Pandilla) de tamaño máximo.

b) Encontrar una cubierta de vértices de tamaño mínimo

c) ¿Existe un ciclo hamiltoniano? Si lo hay, muéstrelo.

d) ¿Cuál es el número mínimo de colores que nos permite colorear el grafo? (Sin que dos nodos del mismo color sean adyacentes)

e) ¿Cuál es el conjunto más grande de vértices que no están conectados entre sí en el grafo?