Data Structures and Algorithms: Hash Tables

Data Structures and Algorithms

8.3 Hash Tables

8.3.1 Direct Address Tables

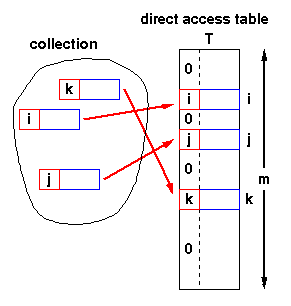
If we have a collection of n elements whose keys are unique integers in (1,m), where m >= n,
then we can store the items in a direct address table, T[m],
where T_i is either empty or contains one of the elements of our collection.

Searching a direct address table is clearly an O(1) operation:
for a key, k, we access T_k,

if it contains an element, return it,
if it doesn't then return a NULL.

There are two constraints here:

the keys must be unique, and
the range of the key must be severely bounded.

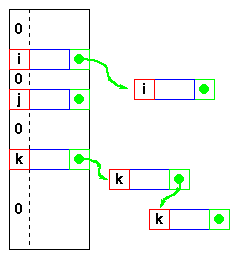
If the keys are not unique, then we can simply construct a set of m lists and store the heads of these lists in the direct address table. The time to find an element matching an input key will still be O(1).
However, if each element of the collection has some other distinguishing feature (other than its key), and if the maximum number of duplicates is n_dup^max, then searching for a specific element is O(n_dup^max). If duplicates are the exception rather than the rule, then n_dup^max is much smaller than n and a direct address table will provide good performance. But if n_dup^max approaches n, then the time to find a specific element is O(n) and a tree structure will be more efficient.

The range of the key determines the size of the direct address table and may be too large to be practical. For instance it's not likely that you'll be able to use a direct address table to store elements which have arbitrary 32-bit integers as their keys for a few years yet!

Direct addressing is easily generalised to the case where there is a function,

h(k) => (1,m)

which maps each value of the key, k, to the range (1,m). In this case, we place the element in T[h(k)] rather than T[k] and we can search in O(1) time as before.

8.3.2 Mapping functions

The direct address approach requires that the function, h(k), is a one-to-one mapping from each k to integers in (1,m). Such a function is known as a perfect hashing function: it maps each key to a distinct integer within some manageable range and enables us to trivially build an O(1) search time table.

Unfortunately, finding a perfect hashing function is not always possible. Let's say that we can find a hash function, h(k), which maps most of the keys onto unique integers, but maps a small number of keys on to the same integer. If the number of collisions (cases where multiple keys map onto the same integer), is sufficiently small, then hash tables work quite well and give O(1) search times.

Handling the collisions

In the small number of cases, where multiple keys map to the same integer, then elements with different keys may be stored in the same "slot" of the hash table. It is clear that when the hash function is used to locate a potential match, it will be necessary to compare the key of that element with the search key. But there may be more than one element which should be stored in a single slot of the table. Various techniques are used to manage this problem:

chaining,
overflow areas,
re-hashing,
using neighbouring slots (linear probing),
quadratic probing,
random probing, ...

Chaining

One simple scheme is to chain all collisions in lists attached to the appropriate slot. This allows an unlimited number of collisions to be handled and doesn't require a priori knowledge of how many elements are contained in the collection. The tradeoff is the same as with linked lists versus array implementations of collections: linked list overhead in space and, to a lesser extent, in time.

Re-hashing

Re-hashing schemes use a second hashing operation when there is a collision. If there is a further collision, we re-hash until an empty "slot" in the table is found.

The re-hashing function can either be a new function or a re-application of the original one. As long as the functions are applied to a key in the same order, then a sought key can always be located.

Linear probing

One of the simplest re-hashing functions is +1 (or -1), ie on a collision, look in the neighbouring slot in the table. It calculates the new address extremely quickly and may be extremely efficient on a modern RISC processor due to efficient cache utilisation (cf. the discussion of linked list efficiency).

The animation gives you a practical demonstration of the effect of linear probing: it also implements a quadratic re-hash function so that you can compare the difference.

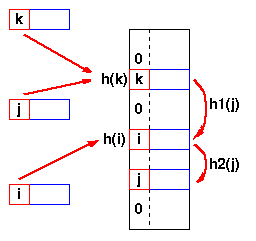
h(j)=h(k), so the next hash function,
h1 is used. A second collision occurs,
so h2 is used.

Clustering

Linear probing is subject to a clustering phenomenon. Re-hashes from one location occupy a block of slots in the table which "grows" towards slots to which other keys hash. This exacerbates the collision problem and the number of re-hashed can become large.

Quadratic Probing

Better behaviour is usually obtained with quadratic probing, where the secondary hash function depends on the re-hash index: address = h(key) + c i² on the t^th re-hash. (A more complex function of i may also be used.) Since keys which are mapped to the same value by the primary hash function follow the same sequence of addresses, quadratic probing shows secondary clustering. However, secondary clustering is not nearly as severe as the clustering shown by linear probes.

Re-hashing schemes use the originally allocated table space and thus avoid linked list overhead, but require advance knowledge of the number of items to be stored.

However, the collision elements are stored in slots to which other key values map directly, thus the potential for multiple collisions increases as the table becomes full.

Overflow area

Another scheme will divide the pre-allocated table into two sections: the primary area to which keys are mapped and an area for collisions, normally termed the overflow area.

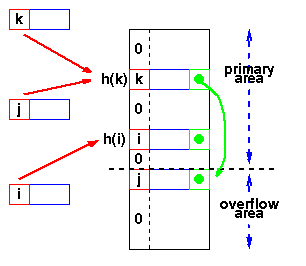When a collision occurs, a slot in the overflow area is used for the new element and a link from the primary slot established as in a chained system. This is essentially the same as chaining, except that the overflow area is pre-allocated and thus possibly faster to access. As with re-hashing, the maximum number of elements must be known in advance, but in this case, two parameters must be estimated: the optimum size of the primary and overflow areas.

Of course, it is possible to design systems with multiple overflow tables, or with a mechanism for handling overflow out of the overflow area, which provide flexibility without losing the advantages of the overflow scheme.

Summary: Hash Table Organization

Organization	Advantages	Disadvantages
Chaining	Unlimited number of elements Unlimited number of collisions	Overhead of multiple linked lists
Re-hashing	Fast re-hashing Fast access through use of main table space	Maximum number of elements must be known Multiple collisions may become probable
Overflow area	Fast access Collisions don't use primary table space	Two parameters which govern performance need to be estimated

Animation

Hash Table Animation
This animation was written by Woi Ang.

Please email comments to:
morris@ee.uwa.edu.au

Key Terms

hash table: Tables which can be searched for an item in O(1) time using a hash function to form an address from the key.
hash function: Function which, when applied to the key, produces a integer which can be used as an address in a hash table.
collision: When a hash function maps two different keys to the same table address, a collision is said to occur.
linear probing: A simple re-hashing scheme in which the next slot in the table is checked on a collision.
quadratic probing: A re-hashing scheme in which a higher (usually 2^nd) order function of the hash index is used to calculate the address.
clustering.: Tendency for clusters of adjacent slots to be filled when linear probing is used.
secondary clustering.: Collision sequences generated by addresses calculated with quadratic probing.
perfect hash function: Function which, when applied to all the members of the set of items to be stored in a hash table, produces a unique set of integers within some suitable range.