These diagrams show how a Huffman encoding tree is built
using a straight-forward greedy algorithm which combines the
two smallest-weight trees at every step.
 |
Initial data sorted by frequency |
 |
Combine the two lowest frequencies,
F and E, to form a sub-tree
of weight 14.
Move it into its correct place. |
 |
Again combine the two lowest frequencies,
C and B, to form a sub-tree
of weight 25.
Move it into its correct place. |
 |
Now the sub-tree with weight, 14, and
D are combined to make a tree of
weight, 30.
Move it to its correct place. |
 |
Now the two lowest weights are held by the
"25" and "30" sub-trees, so combine them to
make one of weight, 55.
Move it after the A. |
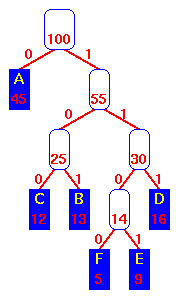 |
Finally, combine the A and the
"55" sub-tree to produce the final tree.
The encoding table is:
A 0
C 100
B 101
F 1100
E 1101
D 111
|





