The following sequence of diagrams illustrates Kruskal's algorithm in operation.

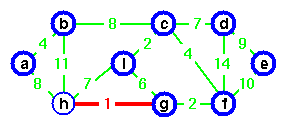
	gh is shortest. Either g or h could be the representative, g chosen arbitrarily.
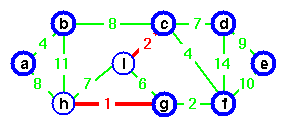
	ci creates two trees. c chosen as representative for second.
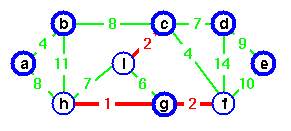
	fg is next shortest. Add it, choose g as representative.
	ab creates a 3rd tree
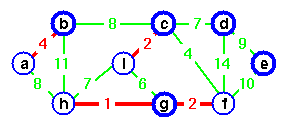
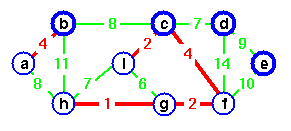
	Add cf, merging two trees. c is chosen as the representative.
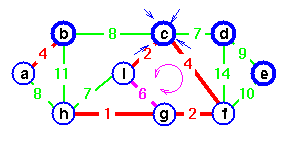
	gi is next cheapest, but a cycle would be created. c is the representative of both.
	Add cd instead
	hi would make a cycle
	Add ah instead
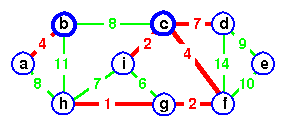
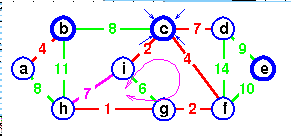
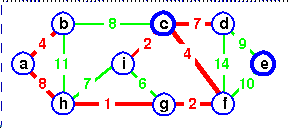
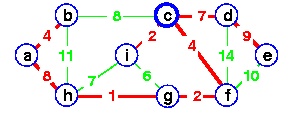
	bc would create a cycle. Add de instead to complete the spanning tree - all trees joined, c is sole representative.

Back to Mininum Spanning Tree

Back to the Table of Contents

© John Morris, 1998