Hash Tables

Hash tables are a simple and effective method to implement dictionaries. Average time to search for an element is O(1), while worst-case time is O(n). Cormen [1990] and Knuth [1998] both contain excellent discussions on hashing.

Theory

A hash table is simply an array that is addressed via a hash function. For example, in Figure 3-1, HashTable is an array with 8 elements. Each element is a pointer to a linked list of numeric data. The hash function for this example simply divides the data key by 8, and uses the remainder as an index into the table. This yields a number from 0 to 7. Since the range of indices for HashTable is 0 to 7, we are guaranteed that the index is valid.

Figure 3-1: A Hash Table

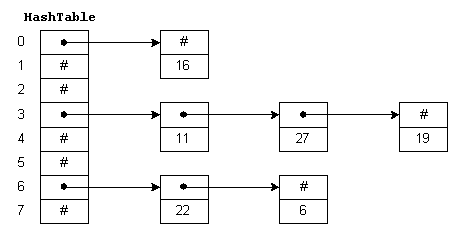
To insert a new item in the table, we hash the key to determine which list the item goes on, and then insert the item at the beginning of the list. For example, to insert 11, we divide 11 by 8 giving a remainder of 3. Thus, 11 goes on the list starting at HashTable[3]. To find a number, we hash the number and chain down the correct list to see if it is in the table. To delete a number, we find the number and remove the node from the linked list.

Entries in the hash table are dynamically allocated and entered on a linked list associated with each hash table entry. This technique is known as chaining. An alternative method, where all entries are stored in the hash table itself, is known as direct or open addressing and may be found in the references.

If the hash function is uniform, or equally distributes the data keys among the hash table indices, then hashing effectively subdivides the list to be searched. Worst-case behavior occurs when all keys hash to the same index. Then we simply have a single linked list that must be sequentially searched. Consequently, it is important to choose a good hash function. Several methods may be used to hash key values. To illustrate the techniques, I will assume unsigned char is 8-bits, unsigned short int is 16-bits and unsigned long int is 32-bits.

Division method (tablesize = prime). This technique was used in the preceeding example. A HashValue, from 0 to (HashTableSize - 1), is computed by dividing the key value by the size of the hash table and taking the remainder. For example:
typedef int HashIndexType; HashIndexType Hash(int Key) { return Key % HashTableSize; }
Selecting an appropriate HashTableSize is important to the success of this method. For example, a HashTableSize of two would yield even hash values for even Keys, and odd hash values for odd Keys. This is an undesirable property, as all keys would hash to the same value if they happened to be even. If HashTableSize is a power of two, then the hash function simply selects a subset of the Key bits as the table index. To obtain a more random scattering, HashTableSize should be a prime number not too close to a power of two.
Multiplication method (tablesize = 2ⁿ). The multiplication method may be used for a HashTableSize that is a power of 2. The Key is multiplied by a constant, and then the necessary bits are extracted to index into the table. Knuth recommends using the fractional part of the product of the key and the golden ratio, or (sqrt(5) - 1)/2. For example, assuming a word size of 8 bits, the golden ratio is multiplied by 2⁸ to obtain 158. The product of the 8-bit key and 158 results in a 16-bit integer. For a table size of 2⁵ the 5 most significant bits of the least significant word are extracted for the hash value. The following definitions may be used for the multiplication method:
/* 8-bit index */ typedef unsigned char HashIndexType; static const HashIndexType K = 158; /* 16-bit index */ typedef unsigned short int HashIndexType; static const HashIndexType K = 40503; /* 32-bit index */ typedef unsigned long int HashIndexType; static const HashIndexType K = 2654435769; /* w=bitwidth(HashIndexType), size of table=2**m */ static const int S = w - m; HashIndexType HashValue = (HashIndexType)(K * Key) >> S;
For example, if HashTableSize is 1024 (2¹⁰), then a 16-bit index is sufficient and S would be assigned a value of 16 - 10 = 6. Thus, we have:
typedef unsigned short int HashIndexType; HashIndexType Hash(int Key) { static const HashIndexType K = 40503; static const int S = 6; return (HashIndexType)(K * Key) >> S; }
Variable string addition method (tablesize = 256). To hash a variable-length string, each character is added, modulo 256, to a total. A HashValue, range 0-255, is computed.
typedef unsigned char HashIndexType; HashIndexType Hash(char *str) { HashIndexType h = 0; while (*str) h += *str++; return h; }
Variable string exclusive-or method (tablesize = 256). This method is similar to the addition method, but successfully distinguishes similar words and anagrams. To obtain a hash value in the range 0-255, all bytes in the string are exclusive-or'd together. However, in the process of doing each exclusive-or, a random component is introduced.
typedef unsigned char HashIndexType; unsigned char Rand8[256]; HashIndexType Hash(char *str) { unsigned char h = 0; while (*str) h = Rand8[h ^ *str++]; return h; }
Rand8 is a table of 256 8-bit unique random numbers. The exact ordering is not critical. The exclusive-or method has its basis in cryptography, and is quite effective (Pearson [1990]).
Variable string exclusive-or method (tablesize <= 65536). If we hash the string twice, we may derive a hash value for an arbitrary table size up to 65536. The second time the string is hashed, one is added to the first character. Then the two 8-bit hash values are concatenated together to form a 16-bit hash value.

typedef unsigned short int HashIndexType; unsigned char Rand8[256]; HashIndexType Hash(char *str) { HashIndexType h; unsigned char h1, h2; if (*str == 0) return 0; h1 = *str; h2 = *str + 1; str++; while (*str) { h1 = Rand8[h1 ^ *str]; h2 = Rand8[h2 ^ *str]; str++; } /* h is in range 0..65535 */ h = ((HashIndexType)h1 << 8)|(HashIndexType)h2; /* use division method to scale */ return h % HashTableSize }

Assuming n data items, the hash table size should be large enough to accommodate a reasonable number of entries. As seen in Table 3-1, a small table size substantially increases the average time to find a key. A hash table may be viewed as a collection of linked lists. As the table becomes larger, the number of lists increases, and the average number of nodes on each list decreases. If the table size is 1, then the table is really a single linked list of length n. Assuming a perfect hash function, a table size of 2 has two lists of length n/2. If the table size is 100, then we have 100 lists of length n/100. This considerably reduces the length of the list to be searched. There is considerable leeway in the choice of table size.

Table 3-1: HashTableSize vs. Average Search Time (µs), 4096 entries

size time size time

1 869 128 9
2 432 256 6
4 214 512 4
8 106 1024 4
16 54 2048 3
32 28 4096 3
64 15 8192 3

Table 3-1: HashTableSize vs. Average Search Time (µs), 4096 entries
size	time	size	time
1	869	128	9
2	432	256	6
4	214	512	4
8	106	1024	4
16	54	2048	3
32	28	4096	3
64	15	8192	3

Implementation

An ANSI-C implementation of a hash table is included. Typedef T and comparison operator compEQ should be altered to reflect the data stored in the table. The hashTableSize must be determined and the hashTable allocated. The division method was used in the hash function. Function insertNode allocates a new node and inserts it in the table. Function deleteNode deletes and frees a node from the table. Function findNode searches the table for a particular value.