Introduction

Arrays and linked lists are two basic data structures used to store information. We may wish to search, insert or delete records in a database based on a key value. This section examines the performance of these operations on arrays and linked lists.

Arrays

Figure 1-1 shows an array, seven elements long, containing numeric values. To search the array sequentially, we may use the algorithm in Figure 1-2. The maximum number of comparisons is 7, and occurs when the key we are searching for is in A[6].


Figure 1-1: An Array

Figure 1-2: Sequential Search

 
int function SequentialSearch (Array A, int Lb, int Ub, int Key);
  begin
  for i = Lb to Ub do
    if A(i) =  Key then
      return i;
    return -1;
  end;

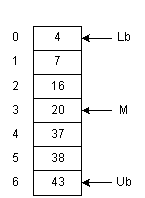
If the data is sorted, a binary search may be done (Figure 1-3). Variables Lb and Ub keep track of the lower bound and upper bound of the array, respectively. We begin by examining the middle element of the array. If the key we are searching for is less than the middle element, then it must reside in the top half of the array. Thus, we set Ub to (M - 1). This restricts our next iteration through the loop to the top half of the array. In this way, each iteration halves the size of the array to be searched. For example, the first iteration will leave 3 items to test. After the second iteration, there will be 1 item left to test. Therefore it takes only three iterations to find any number.

This is a powerful method. Given an array of 1023 elements, we can narrow the search to 511 items in one comparison. Another comparison, and we're looking at only 255 elements. In fact, we can search the entire array in only 10 comparisons.

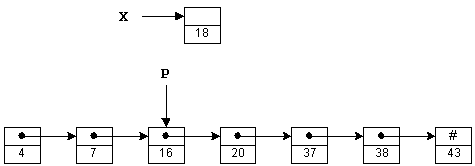
In addition to searching, we may wish to insert or delete entries. Unfortunately, an array is not a good arrangement for these operations. For example, to insert the number 18 in Figure 1-1, we would need to shift A[3]...A[6] down by one slot. Then we could copy number 18 into A[3]. A similar problem arises when deleting numbers. To improve the efficiency of insert and delete operations, linked lists may be used.

Figure 1-3: Binary Search

 
int function BinarySearch (Array A, int Lb, int Ub, int Key);
  begin
  do forever
    M = (Lb + Ub)/2;
    if (Key < A[M]) then
      Ub = M - 1;
    else if (Key > A[M]) then
      Lb = M + 1;
    else
      return M;
    if (Lb > Ub) then
      return -1;
  end;

Linked Lists

In Figure 1-4, we have the same values stored in a linked list. Assuming pointers X and P, as shown in the figure, value 18 may be inserted as follows: 
X->Next = P->Next;
P->Next = X;
Insertion and deletion operations are very efficient using linked lists. You may be wondering how pointer P was set in the first place. Well, we had to do a sequential search to find the insertion point X. Although we improved our performance for insertion/deletion, it has been at the expense of search time.


Figure 1-4: A Linked List

Timing Estimates

Several methods may be used to compare the performance of algorithms. One way is simply to run several tests for each algorithm and compare the timings. Another way is to estimate the time required. For example, we may state that search time is O(n) (big-oh of n). This means that search time, for large n, is proportional to the number of items n in the list. Consequently, we would expect search time to triple if our list increased in size by a factor of three. The big-O notation does not describe the exact time that an algorithm takes, but only indicates an upper bound on execution time within a constant factor. If an algorithm takes O(n2) time, then execution time grows no worse than the square of the size of the list.

Table 1-1: Growth Rates
nlg nn lg nn1.25n2
1 0 0 1 1
16 4 64 32 256
256 8 2,048 1,024 65,536
4,096 12 49,152 32,768 16,777,216
65,536 16 1,048,565 1,048,4764,294,967,296
1,048,476 20 20,969,520 33,554,4321,099,301,922,576
16,775,616 24402,614,7841,073,613,825281,421,292,179,456

Table 1-1 illustrates growth rates for various functions. A growth rate of O(lg n) occurs for algorithms similar to the binary search. The lg (logarithm, base 2) function increases by one when n is doubled. Recall that we can search twice as many items with one more comparison in the binary search. Thus the binary search is a O(lg n) algorithm.

If the values in Table 1-1 represented microseconds, then a O(lg n) algorithm may take 20 microseconds to process 1,048,476 items, a O(n1.25) algorithm might take 33 seconds, and a O(n2) algorithm might take up to 12 days! In the following chapters a timing estimate for each algorithm, using big-O notation, will be included. For a more formal derivation of these formulas you may wish to consult the references.

Summary

As we have seen, sorted arrays may be searched efficiently using a binary search. However, we must have a sorted array to start with. In the next section various ways to sort arrays will be examined. It turns out that this is computationally expensive, and considerable research has been done to make sorting algorithms as efficient as possible.

Linked lists improved the efficiency of insert and delete operations, but searches were sequential and time-consuming. Algorithms exist that do all three operations efficiently, and they will be the discussed in the section on dictionaries.