Quicksort

Although the shell sort algorithm is significantly better than insertion sort, there is still room for improvement. One of the most popular sorting algorithms is quicksort. Quicksort executes in O(n lg n) on average, and O(n²) in the worst-case. However, with proper precautions, worst-case behavior is very unlikely. Quicksort is a non-stable sort. It is not an in-place sort as stack space is required. For further reading, consult Cormen [1990].

Theory

The quicksort algorithm works by partitioning the array to be sorted, then recursively sorting each partition. In Partition (Figure 2-3), one of the array elements is selected as a pivot value. Values smaller than the pivot value are placed to the left of the pivot, while larger values are placed to the right.

Figure 2-3: Quicksort Algorithm

int function Partition (Array A, int Lb, int Ub); begin select a pivot from A[Lb]...A[Ub]; reorder A[Lb]...A[Ub] such that: all values to the left of the pivot are <= pivot all values to the right of the pivot are >= pivot return pivot position; end; procedure QuickSort (Array A, int Lb, int Ub); begin if Lb < Ub then M = Partition (A, Lb, Ub); QuickSort (A, Lb, M - 1); QuickSort (A, M + 1, Ub); end;

Figure 2-3: Quicksort Algorithm
int function Partition (Array A, int Lb, int Ub); begin select a pivot from A[Lb]...A[Ub]; reorder A[Lb]...A[Ub] such that: all values to the left of the pivot are <= pivot all values to the right of the pivot are >= pivot return pivot position; end; procedure QuickSort (Array A, int Lb, int Ub); begin if Lb < Ub then M = Partition (A, Lb, Ub); QuickSort (A, Lb, M - 1); QuickSort (A, M + 1, Ub); end;

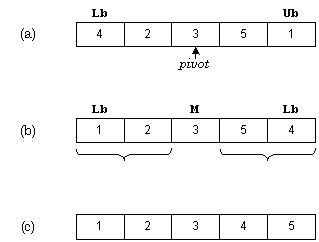
In Figure 2-4(a), the pivot selected is 3. Indices are run starting at both ends of the array. One index starts on the left and selects an element that is larger than the pivot, while another index starts on the right and selects an element that is smaller than the pivot. In this case, numbers 4 and 1 are selected. These elements are then exchanged, as is shown in Figure 2-4(b). This process repeats until all elements to the left of the pivot <= the pivot, and all elements to the right of the pivot are >= the pivot. QuickSort recursively sorts the two subarrays, resulting in the array shown in Figure 2-4(c).

Figure 2-4: Quicksort Example

As the process proceeds, it may be necessary to move the pivot so that correct ordering is maintained. In this manner, QuickSort succeeds in sorting the array. If we're lucky the pivot selected will be the median of all values, equally dividing the array. For a moment, let's assume that this is the case. Since the array is split in half at each step, and Partition must eventually examine all n elements, the run time is O(n lg n).

To find a pivot value, Partition could simply select the first element (A[Lb]). All other values would be compared to the pivot value, and placed either to the left or right of the pivot as appropriate. However, there is one case that fails miserably. Suppose the array was originally in order. Partition would always select the lowest value as a pivot and split the array with one element in the left partition, and Ub - Lb elements in the other. Each recursive call to quicksort would only diminish the size of the array to be sorted by one. Therefore n recursive calls would be required to do the sort, resulting in a O(n²) run time. One solution to this problem is to randomly select an item as a pivot. This would make it extremely unlikely that worst-case behavior would occur.

Implementation

An ANSI-C implementation for quicksort is included. Typedef T and comparison operator compGT should be altered to reflect the data stored in the array. Several enhancements have been made to the basic quicksort algorithm:

The center element is selected as a pivot in partition. If the list is partially ordered, this will be a good choice. Worst-case behavior occurs when the center element happens to be the largest or smallest element each time partition is invoked.
For short arrays, insertSort is called. Due to recursion and other overhead, quicksort is not an efficient algorithm to use on small arrays. Consequently, any array with fewer than 12 elements is sorted using an insertion sort. The optimal cutoff value is not critical and varies based on the quality of generated code.
Tail recursion occurs when the last statement in a function is a call to the function itself. Tail recursion may be replaced by iteration, resulting in a better utilization of stack space. This has been done with the second call to QuickSort in Figure 2-3.
After an array is partitioned, the smallest partition is sorted first. This results in a better utilization of stack space, as short partitions are quickly sorted and dispensed with.

Also included is an ANSI-C implementation, of qsort, a standard C library function usually implemented with quicksort. Recursive calls were replaced by explicit stack operations. Table 2-1, shows timing statistics and stack utilization before and after the enhancements were applied.

Table 2-1: Effect of Enhancements on Speed and Stack Utilization

count time (µs) stacksize

before after before after

16 103 51 540 28

256 1,630 911 912 112

4,096 34,183 20,016 1,908 168

65,536 658,003 460,737 2,436 252

count	time (µs)		stacksize
count	before	after	before	after
16	103	51	540	28
256	1,630	911	912	112
4,096	34,183	20,016	1,908	168
65,536	658,003	460,737	2,436	252