Red-Black Trees
Binary search trees work best when they are balanced or the path
length from root to any leaf is within some bounds. The red-black
tree algorithm is a method for balancing trees. The name
derives from the fact that each node is colored red or black, and
the color of the node is instrumental in determining the balance
of the tree. During insert and delete operations, nodes may be
rotated to maintain tree balance. Both average and worst-case
search time is O(lg n). For details, consult
Cormen [1990].
Theory
A red-black tree is a balanced binary search tree with the
following properties:
- Every node is colored red or black.
- Every leaf is a NIL node, and is colored black.
- If a node is red, then both its children are black.
- Every simple path from a node to a descendant leaf contains
the same number of black nodes.
The number of black nodes on a path from root to leaf is known as
the black-height of a tree. These properties guarantee that any
path from the root to a leaf is no more than twice as long as any
other. To see why this is true, consider a tree with a black
height of two. The shortest distance from root to leaf is two,
where both nodes are black. The longest distance from root to
leaf is four, where the nodes are colored (root to leaf): red,
black, red, black. It is not possible to insert more black nodes
as this would violate property 4, the black-height requirement.
Since red nodes must have black children (property 3), having two
red nodes in a row is not allowed. The largest path we can
construct consists of an alternation of red-black nodes, or twice
the length of a path containing only black nodes. All operations
on the tree must maintain the properties listed above. In
particular, operations which insert or delete items from the tree
must abide by these rules.
Insertion
To insert a node, we search the tree for an insertion point, and
add the node to the tree.
A new node replaces an existing NIL node at the bottom of the tree,
and has two NIL nodes as children. In the implementation, a NIL
node is simply a pointer to a common sentinel node that is colored black.
After insertion, the new node
is colored red. Then the parent of the node is examined to
determine if the red-black tree properties have been violated.
If necessary, we recolor the node and do rotations to balance the
tree.
By inserting a red node
with two NIL children, we have preserved black-height
property (property 4). However, property 3 may be violated.
This property states that both children of a red node must be
black. Although both children of the new node are black (they're
NIL), consider the case where the parent of the new node is red.
Inserting a red node under a red parent would violate this
property. There are two cases to consider:
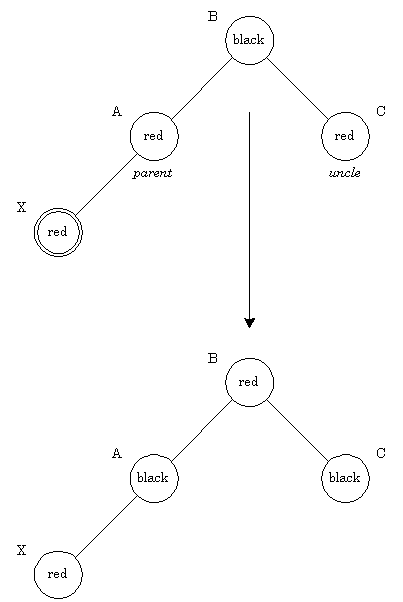
- Red parent, red uncle:
Figure 3-6 illustrates a red-red
violation. Node X is the newly inserted node, with both parent
and uncle colored red. A simple recoloring removes the red-red
violation. After recoloring, the grandparent (node B) must be
checked for validity, as its parent may be red. Note that this
has the effect of propagating a red node up the tree. On
completion, the root of the tree is marked black. If it was
originally red, then this has the effect of increasing the black-height
of the tree.
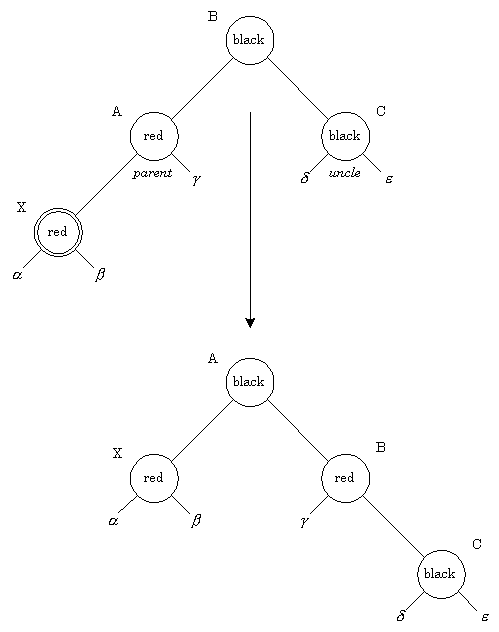
- Red parent, black uncle:
Figure 3-7 illustrates a red-red
violation, where the uncle is colored black. Here the nodes may
be rotated, with the subtrees adjusted as shown. At this point
the algorithm may terminate as there are no red-red conflicts and
the top of the subtree (node A) is colored black. Note that if
node X was originally a right child, a left rotation would be
done first, making the node a left child.
Each adjustment made while inserting a node causes us to travel
up the tree one step. At most 1 rotation (2 if the node is a
right child) will be done, as the algorithm terminates in this
case. The technique for deletion is similar.
Implementation
An
ANSI-C implementation
for red-black trees is included.
Typedef T and comparison operators compLT
and compEQ should be altered to reflect the data stored in the
tree. Each Node consists of left, right, and parent pointers
designating each child and the parent. The node color is stored
in color, and is either RED or BLACK. The data is stored in the
data field. All leaf nodes of the tree are sentinel nodes, to
simplify coding. The tree is based at root, and initially is a
sentinel node.
Function insertNode allocates a new node and inserts it in the tree.
Subsequently, it calls insertFixup to ensure that the red-black
tree properties are maintained. Function
deleteNode deletes a node from
the tree. To maintain red-black tree properties, deleteFixup is
called. Function findNode searches the tree for a particular value.