Shell Sort

Shell sort, developed by Donald L. Shell, is a non-stable in-place sort. Shell sort improves on the efficiency of insertion sort by quickly shifting values to their destination. Average sort time is O(n^1.25), while worst-case time is O(n^1.5). For further reading, consult Knuth [1998].

Theory

In Figure 2-2(a) we have an example of sorting by insertion. First we extract 1, shift 3 and 5 down one slot, and then insert the 1, for a count of 2 shifts. In the next frame, two shifts are required before we can insert the 2. The process continues until the last frame, where a total of 2 + 2 + 1 = 5 shifts have been made.

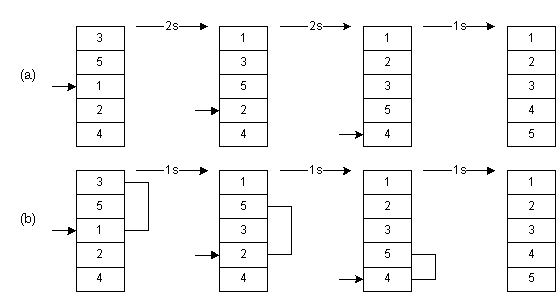
In Figure 2-2(b) an example of shell sort is illustrated. We begin by doing an insertion sort using a spacing of two. In the first frame we examine numbers 3-1. Extracting 1, we shift 3 down one slot for a shift count of 1. Next we examine numbers 5-2. We extract 2, shift 5 down, and then insert 2. After sorting with a spacing of two, a final pass is made with a spacing of one. This is simply the traditional insertion sort. The total shift count using shell sort is 1+1+1 = 3. By using an initial spacing larger than one, we were able to quickly shift values to their proper destination.

Figure 2-2: Shell Sort

Various spacings may be used to implement a shell sort. Typically the array is sorted with a large spacing, the spacing reduced, and the array sorted again. On the final sort, spacing is one. Although the shell sort is easy to comprehend, formal analysis is difficult. In particular, optimal spacing values elude theoreticians. Knuth has experimented with several values and recommends that spacing h for an array of size N be based on the following formula:

Let h₁ = 1, h_s+1 = 3h_s + 1, and stop with h_t when h_t+2 >= N.

Thus, values of h are computed as follows:

h₁ = 1
h₂ = (3 x 1) + 1 = 4
h₃ = (3 x 4) + 1 = 13
h₄ = (3 x 13) + 1 = 40
h₅ = (3 x 40) + 1 = 121

To sort 100 items we first find an h_s such that h_s >= 100. For 100 items, h₅ is selected. Our final value (h_t) is two steps lower, or h₃. Therefore our sequence of h values will be 13-4-1. Once the initial h value has been determined, subsequent values may be calculated using the formula

h_s-1 = floor(h_s / 3).

Implementation

An ANSI-C implementation for shell sort is included. Typedef T and comparison operator compGT should be altered to reflect the data stored in the array. The central portion of the algorithm is an insertion sort with a spacing of h.