Postfix Notation Mini-Lecture

Postfix Notation

Mini-Lecture

Bob Brown
School of Computing and Software Engineering
Southern Polytechnic State University
Copyright � 2001 by Bob Brown

For students of computer architecture this postfix notation mini-lecture is really an aside to show you how mind-bogglingly useful the concept of a stack is. It doesn't make any difference whether the stack is implemented in hardware and supported by the microarchitecture or simulated using an array and totally a creation of the high-level language programmer.

At some point in your career you will be asked to write a program that can interpret an expression in a notation similar to that of algebra. Getting something like (A+B)/(C-D) right can seem like a daunting task, especially when you are asked to write code that will interpret any valid expression. It turns out to be surprisingly easy if the program is decomposed into two steps: translation to postfix notation and evaluation of the postfix notation expression. This is not a new idea... it was described by Donald Knuth in 1962 [KNUT62] and he was writing a history!

Postfix Notation

Postfix notation is a way of writing algebraic expressions without the use of parentheses or rules of operator precedence. The expression above would be written as AB+CD-/ in postfix notation. (Don't panic! We'll explain this in a moment.) Postfix notation was introduced by Jan Lukasiewicz (1878-1956), a Polish logician, mathematician, and philosopher. Lukasiewicz developed a parenthesis-free prefix notation that came to be called Polish notation and a postfix notation called reverse Polish notation, or RPN.

In this mini-lecture we will use variables represented by single letters and operators represented by single characters. Things are more complicated in real life. Variables have names composed of many characters and some operators, like ** for exponentiation, require more than a single character. However, we can make these simplifications without loss of generality.

In our simplified examples, each variable is represented by a single letter and each operator by a single character. These are called tokens. In a more complex implementation, your program would still scan a series of tokens, but they would likely be pointers into symbol tables, constant pools, and procedure calls for operators.

Evaluating Postfix Notation

Evaluating an expression in postfix notation is trivially easy if you use a stack. The postfix expression to be evaluated is scanned from left to right. Variables or constants are pushed onto the stack. When an operator is encountered, the indicated action is performed using the top elements of the stack, and the result replaces the operands on the stack.

Let's do an example using the postfix expression AB+CD-/. In order to see what's going on as the expression is evaluated, we will substitute numbers for the variables. The expression to be evaluated becomes 9 7 + 5 3 - /. This is equivalent to (9 + 7) / (5 - 3) so we expect the answer to be eight. Click the "Go" button at the right to see an animation showing the evaluation of the expression.

You will see the expression scanned from left to right. A yellow highlight shows the term currently being scanned. The digits in the expression are pushed onto the stack and the operators are performed.

Experiment with the animation until you are sure you understand what's going on.

Now that you see how easy it is to evaluate an expression that's in RPN form, you will want to convert ordinary infix expressions to RPN so that you can evaluate them. That turns out to be easy, too, if you use a stack.
�

Converting Infix to Postfix

We know that the infix expression (A+B)/(C-D) is equivalent to the postfix expression AB+CD-/. Let's convert the former to the latter.

We have to know the rules of operator precedence in order to convert infix to postfix. The operations + and - have the same precedence. Multiplication and division, which we will represent as * and / also have equal precedence, but both have higher precedence than + and -. These are the same rules you learned in high school.

We place a "terminating symbol" after the infix expression to serve as a marker that we have reached the end of the expression. We also push this symbol onto the stack.

After that, the expression is processed according to the following rules:

Variables (in this case letters) are copied to the output
Left parentheses are always pushed onto the stack
When a right parenthesis is encountered, the symbol at the top of the stack is popped off the stack and copied to the output until the symbol at the top of the stack is a left parenthesis. When that occurs, both parentheses are discarded.
If the symbol being scanned has a higher precedence than the symbol at the top of the stack, the symbol being scanned is pushed onto the stack.
If the precedence of the symbol being scanned is lower than or equal to the precedence of the symbol at the top of the stack, the stack is popped to the output.
When the terminating symbol is reached on the input scan, the stack is popped to the output until the terminating symbol is also reached on the stack. Then the algorithm terminates.
If the top of the stack is a left parenthesis and the terminating symbol is scanned, or a right parenthesis is scanned when the terminating symbol is at the top of the stack, the parentheses of the original expression were unbalanced and an unrecoverable error has occurred.

Click the "go" button on the animation to see how (A+B)/(C-D) is transformed to the postfix expression AB+CD-/. You can use "reset" and "go" to run the animation several times.

When an infix expression has been converted to postfix, the variables are in the same order. However, the operators have been reordered so that they are executed in order of precedence.

Understanding Table 5-21 in Tanenbaum

The rules expressed as a list in the previous section are shown in a nice, unambiguous table in Structured Computer Organization by Andrew Tanenbaum. [TANE99] Unfortunately, for some students the "train" analogy gets in the way of seeing how to use this table. Here is the material on pp. 339-340 of Tanenbaum presented in terms of a stack rather than with the train analogy.

The terminating symbol is appended to the expression to be converted and also pushed onto the stack.
The expression is scanned left-to-right.
If a variable is encountered, it is copied to the output.
If a symbol is encountered, it is compared with the symbol at the stop of the stack using Table 5-21, and one of the following actions is taken depending on the number from the table:
1. The symbol being scanned is pushed onto the stack.
2. The stack is popped and the symbol from the stack is copied to the output.
3. Both the symbol being scanned and the symbol at the top of the stack are deleted. (This is how parentheses are removed from the infix expression.)
4. Done. The expression has been converted and the algorithm terminates successfully.
5. Error. The parentheses in the original expression were not balanced, and the expression cannot be converted.
After each action is taken, an new comparison is made between the symbol being scanned, which may be the same as in the previous comparison, and the symbol at the top of the stack. This continues until the algorithm terminates.

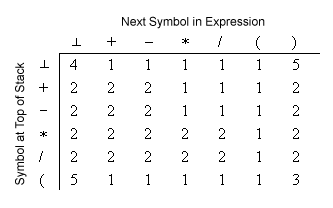Figure 5-21 from [TANE99]. Find the symbol at the top of the stack on the left and the symbol being scanned across the top. The action to take is indicated by the number at the intersection of the row and column.

�

Please take a moment to provide comments on this MiniLecture.

Table of Contents

Revised: Thu, 13 Mar 2003 02:48:44 GMT

References

[KNUT62] Knuth, Donald E., "A History of Writing Compilers," Computers and Automation,, December, 1962, reprinted in Pollock, Bary w., ed. Compiler Techniques, AUERBACH Publishers, 1972.

[TANE99] Tanenbaum, Andrew S., Structured Computer Organization, Prentice-Hall, 1999.