Diseño
y Programación Orientados a Objetos
1er. Sem 2012
Tarea 1: Bolas Móviles en Espacio Cerrado como Objetos de Software
Recomendación: Lea detenidamente la tarea. Si algo no lo
entiende, consulte en clases. Si es preciso, se incorporarán
aclaraciones al final.
Esta tarea tiene por objetivos:
* Ejercitar la configuración de un ambiente de trabajo para desarrollo
de aplicaciones en lenguaje Java (se ha sugerido trabajar con Jgrasp, Eclipse o NetBeans )
* Reconocer objetos de software como modelos de objetos reales.
* Reconocer clases y relaciones entre ellas en códigos fuentes Java.
* Ejercitar el diseño e implementación de una clase simple (Vector2D).
* Ejercitar la extensión de clases dadas para satisfacer nuevos requerimientos.
* Ejercitar la entrada y salida de datos.
* Conocer el formato .csv y su importación a planillas electrónicas.
* Ejercitar la preparación y entrega de resultados de software
(creación de readme, documentación y agrupación de una
colección de archivos en uno "tar").
* Aprender una estrategia para programar simulaciones de fenómenos continuos.
Descripción General
En esta tarea se modela la interacción objetos reales bolas y
paredes sujetos a las leyes de la "naturaleza". A partir de
estos modelos se construyen clases de software para crear objetos de
software que representarán a los objetos reales. En física usted
estudió colisiones elásticas (conservación de energía además del
momentum). Para calcular su dinámica, en esta tarea las bolas
serán modeladas como esferas sin roce con la superficie. Decimos que
este es un modelo y
no la realidad porque existe roce y éste hace rodar las bolas; sin
embargo,
esta suposición simplificará nuestro planteamiento y nos permitirá
obtener resultados con precisión satisfactoria para nuestros fines.
Además tendremos paredes rectas e infinitas de masa muy grande por lo
cual se mantienen fijas. Estos objetos están inmersos en un
campo de gravedad constante y con una fuerza disipativa (roce de fluido)
que supondremos proporcional a la magnitud de la velocidad y el radio de cada bola.
Una vez que las clases básicas estén definidas, usted creará
instancias de bolas y paredes en el modelo del mundo que estamos describiendo para formar
un experimento a simular. Notar que aquí aparece otro actor:
un
simulador. El simulador no es más que el modelo del paso del tiempo, el
cual será informado a cada objeto. El tiempo avanzará en pasos
discretos en lugar de un continuo y así iremos avanzando en nuestra
simulación de a pasos
"pequeños" (deltas de tiempo). Para calcular la dinámica de bolas sujetas a fuerzas externas, revise este material y éste para los choques.
Esta tarea les pide construir experimentos con bolas chocando en
una superficie horizontal de dos dimensiones y limitada por paredes,
todo en R2. Un ejemplo de tales escenarios se muestra en la Figura 1.
Para ello usted contará con una solución bastante avanzada del problema
en R. Una vez que la configuración esté armada se inicia la
simulación por un tiempo definido por consola. Los resultados,
es decir las posiciones de los cuerpos en el tiempo, serán escritas en pantalla.
Luego usted debe importar sus datos en una planilla electrónica para
generar gráficos del movimiento de sus objetos.
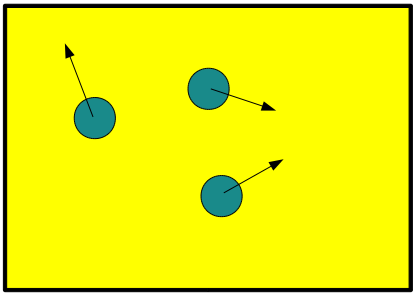
Figura 1: Imagen de un escenario posible en R
2
Resultados Esperados de su Grupo
Si
bien usted puede usar un IDE (Integrated Development Environment),
usted debe saber cómo compilar y correr su tarea dese la línea de
comandos.
Su tarea debe ser ejecutable en aragorn.elo.utfsm.cl usando:
$ java PhysicsLab <delta tiempo> <tiempo total a simular> <periodo de muestreo>
La salida del programa será a pantalla.
Luego el programa corre hasta generar toda la salida indicada. En pantalla debería generar algo del tipo:
Time,
Ball_0: x,y , Ball_1: x,y , Ball_2: x,y , Wall_0:
x , Wall_1: x, Wall_2: y
, Wall_3: y
0.0, 1.0, 3.0 , 2.0 , 3.5,
2.2, 1.0, 0.0 , 5.0 ,
0.0, 4.0
/* aquí omito el resto de las líneas */
Para efectos de esta tarea, el estado de salida sólo incluye las posiciones de cada objeto.
Usted deberá entregar los siguientes archivos:
- readme
- Archivo de Documentación: éste incluye la Figura 2 y un gráfico (x,t)
que muestre la posición y de las bolas como función del tiempo
para 0<t<14[s]. Para este experimento use los datos del
escenario proporcionado en los fuentes. Este archivo además debe
incluir el esquema de la
Figura 1 y un gráfico (X,Y) de la trayectoria de la bola de más a la izquierda
0<t<"tiempo en que ha chocado una vez con otra bola", use los datos iniciales del
ejemplo de salida más arriba, y velocidades que usted elija. g=0.0 [m/s2]; fricción del aire pequeña para lograr el choque pedido. Indique las dificultades
encontradas y cómo las resolvió. Si usted desea analizar otro caso,
puede hacerlo e incluirlo.
- Archivo Vector2D.java donde usted describe su clase para representar vectores en R2.
- Archivo Ball.java donde cada bola opera en un plano de dos dimensiones.
Esta clase debe admitir los mismos constructores del caso en R, pero extendidos a dos dimensiones.
public Ball(float mass, float r, Vector2D position, Vector2D speed, MyWorld world)
- Archivo Wall.java para paredes el plano.
Esta clase debe admitir el siguiente constructor de Bloques:
public public Wall(char axis, float pos, MyWorld world) /* axis puede ser x o y */
La idea de definir estos constructores es que el ayudante puede
construir su propio escenario y usar su implementación para generar
otros resultados.
-
Los archivo PhysicsElement.java, y
MyWorld.java deben ser adaptados a partir de los entregados más abajo.
- Archivo PhysicsLab.java además del main éste contendrá su configuración para el experimento de la Figura 1.

Figura 2: Dos bolas, sin gravedad y sin fricción usando parámetros del código ejemplo.
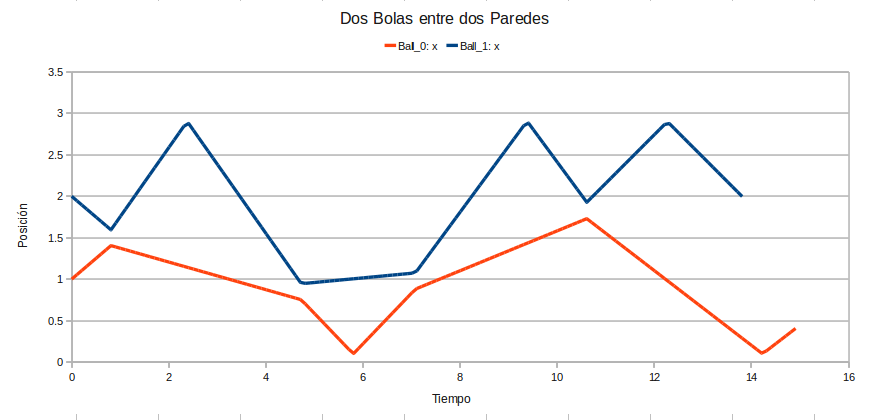
Figura 3: Gráfico para el experimento de la Figura 2.
Ayudas
* Dé una mirada a la solución del problema en R. Si encuentra errores o algo que pueda ser mejorado, avise al profesor.
* Para enviar los datos a un archivo de salida, redireccione la salida a pantalla usando:
$ java PhysicsLab 0.01 15 0.1 > miSalida.csv
Luego trate este archivo como si fuera planilla electrónica. Usted
podrá usar las "comas" y "tabs" como separador de columnas.
* No dude en consultar al profesor o ayudante sobre dudas de esta tarea.
* La
fuerza de fricción con el aire depende el aire y forma del cuerpo. En
esta tarea la modelaremos como proporcional a la velocidad del cuerpo
(es una aproximación válida cuando no hay turbulencias -caso
velocidades bajas). La constante de proporcionalidad la podemos modelar
de dos formas: como constante para todas las masas, o como el producto
de la viscosidad del aire por un factor que depende de la geometría de
cada cuerpo. Si usamos el primer enfoque, la Constante de Roce Viscoso
(viscous friction constant) , será un atributo más de MyWorld (similar
a g). Si usamos el segundo enfoque, podemos asociar la viscosidad del
aire a MyWorld y una constante "crossSection" (sección eficaz) a
cada masa. La Constante de Roce Viscoso en este último caso será el
producto de ambas. Este último modelo es el usado en el código proporcionado.
Nociones de simulación de fenómenos continuos
La idea básica usada en esta tarea es discretizar el tiempo; para cada
instante discreto, congelamos el tiempo y pedimos a cada objeto
del experimento calcular cuál será su estado futuro (delta t más tarde)
a partir del estado actual y las condiciones en que está sometido. Es
importante congelar el tiempo y hacer este cálculo para cada objeto.
Luego pedimos a todos actualizar su estado basado en lo calculado y
avanzamos el tiempo en ese delta. Esta simple idea trabaja bien aquí y
en muchas situaciones.
Una vez hecha la tares, usted debería notar que es posible incorporar gravedad y pensar que el plano R2 es vertical.
Se
puede jugar cambiando los tamaños o el número de bolas involucradas.
Cuando hay muchas bolas, se podría estimar la presión lineal (fuerza
por unidad de longitud) en las paredes. Al analizar todo verticalmente
se debería poder apreciar una mayor concentración de bolas en promedio
en las partes bajas. Por otro lado este ramo no es el único
donde deben rendir bien este semestre.



