y cree un
PhysicsLab.java para generar la gráfica correspondiente a el choque
simple de la Figura A.
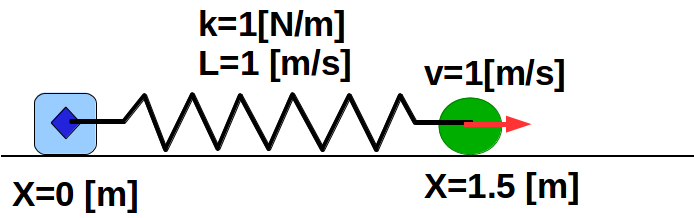
Figura A: 2 Bolas de igual masa, una en
movimiento no acelerado y otra en reposo. Se muestra estado inicial.
Nota: Si lo desea, resuelva primero una bola moviéndose sin
aceleración. Una vez que comprueba que funciona el simulador, la
entrada de datos, salida de datos, cómo hacer gráfica, etc.., agrega
el choque. Para la entrega de esta etapa se pide la configuración
final de la tarea.
Segunda Etapa
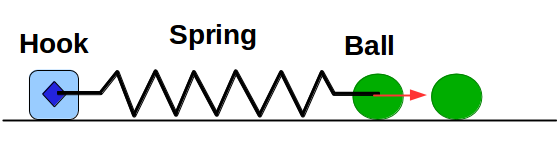
Como segundo paso, complete el
código agregando la clase resorte
(Spring) y cree un PhysicsLab.java que genere los resultados para la
configuración de la Figura B.
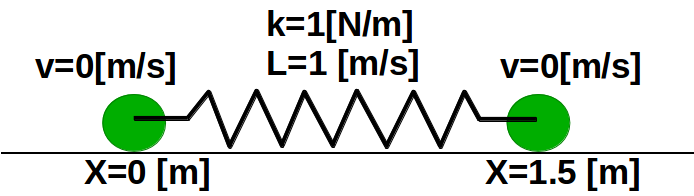
Figura B: 2 bolas en configuración simétrica. Se muestra estado
inicial.