Aproximación Pseudo-Óptima de Imágenes por Polígonos Mediante el Uso de un Algoritmo Genético

Descripción del Problema

Por varias razones, de las cuales no es la menos importante la competitividad del mercado, en ingeniería no solo se buscan soluciones que trabajen a cierto nivel nominal, si no que sean también de cierta manera la mejor solución. O en otras palabras, en ingeniería se enfrentan frecuentemente problemas de optimización.

En el presente trabajo se busca solucionar un problema de optimización particular: La aproximación de imágenes mediante polígonos coloreados. Para esto, el problema será enfrentado desde el marco de los los llamados algortimos genéticos, algoritmo que en este caso será diseñado utilizando las guías provistas por la programación orientada a objetos.

       

Figura 1: ¿Cómo aproximar la imagen de la izquierda mediante una imagen como la de la derecha?

Análisis del Problema

Formulación del problema de optimización

El primer paso para formular un problema de optimización es caracterizar los resultados factibles y el costo que va a representar la elección de cada resultado. En esta caso, se tiene una imagen objetivo $I_{obj}$ a aproximar, por lo cual cualquier aproximación tentativa $I_{app}$ forma parte del espacio de factibilidad. Las aproximaciones solo podrán ser imágenes construidas mediante la superposición de polígonos transparentes. Además, en esta caso consideraremos como aproximaciones válidas  solo aquellas imágenes con las mismas dimensiones de la imagen objetivo.

Se considerará el error el aproximación somo un error cuadrático medio de los pixeles, esto es

$$Error\left(I_{obj},I_{app}\right)=\sum _{i,j}{\left(pi{x}_{i,j}^{obj}-pi{x}_{i,j}^{app}\right)}^2,$$$$Error\left(I_{obj},I_{app}\right) = \sum_{i,j} \left(pix^{obj}_{i,j}-p$$donde $pix^{obj}_{i,j}$ corresponde al pixel en la posición $(i,j)$ de la imágen objetivo, y $pix^{app}_{i,j}$ al pixel en la posición $(i,j)$ de la aproximación.

Los pasos siguientes en la formulación del problema corresponden normalmente a agregar restricciones. Si bien en esta formulación no se considerarán explícitamente restricciones, en la subsección de casos de uso se analizarán las distintas limitaciones intrinsecas al computo de la solución.

Diseño del algoritmo genético

Un algoritmo genético es un método heurístico inspirado por el proceso de selección natural, y utlizado comunmente en la generación de soluciones de alta calidad a problemas de optimización  y busqueda. En el caso del presente trabajo, es utilizado un modelo genético como el mostrado en la Figura 2. En él, un individuo (superviviente) genera un descendiente (nueva generación) afectado por mutaciones. Luego, el individuo que sobrevivirá será aquel que presente un menor error de aproximación, abriendo la posibilidad de ejecutar una nueva iteración.

Cada individuo es caracterizado por su propia cadena de ADN, la cual describe la disposición y el color de los polígonos necesarios para construir la imagen. Así mismo, las mutaciones afectan aleatoria y directamente al ADN del individuo, donde cada mutación válida tiene su propia probabilidad de ocurrencia.

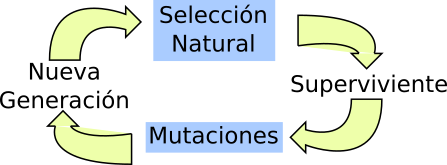
Figura 2: Modelo evolutivo utilzado.

Casos de uso

• Caso de uso 1: Estudio de Desempeño de Tiempo invertido v/s Optimalidad.
  Una de las limitaciones más importantes de el computo de las soluciones es el tiempo diponible. Normalmente el tiempo que se deja corriendo el algoritmo determina la optimalidad del resultado. Pero también se sabe que el tiempo de ejecución implica costos importantes. Entonces, el cómputo de la aproximación implica un compromiso entre el tiempo de ejecución y la optimalidad de la solución.
  Por esta razón, un importante caso de uso es analizar el desempeño del algoritmo genético en terminos de el tiempo de ejecución y la razón de cambio del error de aproximación. Esto le permite al usuario
  
  
• Caso de uso 2: Compresión.
  Un ejemplo clásico y muy útil de problema de optimización es el que implica la compresión de datos. En este contexto, por ejemplo, el usuario puede requerir la compresión de una imágen, codificándola con la pérdida de información que esto implique, en términos de polígonos coloreados. De esta manera, el usuario puede requerir limitar la cantidad de polígonos utilizables y sus vértices, o la cantidad de colores permitidos. Así, por ejemplo, el usuario puede almacenar las imágenes comprimidas en entornos de memoria limitada.
  
  
• Caso de uso 3: Comparación entre las Distintas Mutaciones.
  Con fines de estudio de, se puede analizar el efecto de las distintas mutaciones en la convergencia del algoritmo. Por ejemplo, se puede comparar el efecto de agregar una nueva mutación al sistema, en términos de eficiencia y desempeño.
  
  
  

Implementación

El código del algoritmo fue programado en lenguage python. Además, con el fin de facilitar la interacción con el usuario, el programa se implementó en el entorno Jupyter.

El algoritmo genético es implementado en tres clases: Polygon, ADN y History. La función de cada clase se explica a continuación:

• Clase Polygon: Representa un polígono. Contiene dos atributos. El primero es el atributo "vertex", el cual es un arreglo con la posición de cada vértice del polígono. El segundo atributo especifica el color del polígono. Además la clase contiene los métodos necesarios para aplicar las distintas mutaciones sobre el polígono.
  
• Clase ADN: Contiene la información para construir una imagen mediante polígonos. Contiene principalmente un atributo, que es el arreglo de polígonos que componen una imagen. Contiene además un metodo para mutar el ADN, y el método para calcular el error de aproximación, usando como entrada la imagen objetivo.
• Clase History: Es la clase encargada de ejecutar el algoritmo genético. Contiene como atributo un superviviente y la cantidad de iteraciones a realizar. Contiene solo un método "run", el cual ejecuta la cantidad de iteraciones especificadas, graficando constantemente la evolución del algoritmo.

En la Figura 3 se muestra el diagrama de clases resultante.

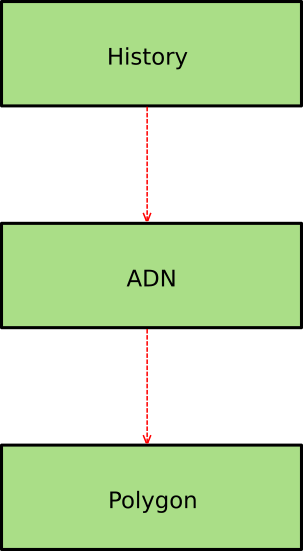
Figura 3: Diagrama de clases de la implementación

Resultados

La imagen objetivo utilizada es aquella en la izquierda de la Figura 1. Se realizaron principalmente tres simulaciones del algortimo. La primera consideró solo el uso de triángulos y mutaciones sue solo afectaron triángulos. La segunda admitió el uso de polígonos con más de tres verticas, y mutaciones que permitieron variar el número de vértices a un polígono. Finalmente, la tercera agregó la posibilidad de mutar cada vértice por separado.

La evolución de las similaciones realizadas se muestra en la Animación 1. La Animación 1 permite comparar como afecta cada cambio en la evolución perceptual del algoritmo.

     

Animación 1: Resultado obtenido en cada una de las tres pruebas realizadas. A la izquerda, se muestra el resultado de aproximar con triángulos. Al centro se muestra el resultado de agregar polígonos. A la derecha se muestra el resultado de agregar la mutación de cada vértice.

Las dificultades encontradas durante el desarrollo del proyecto fueron principalmente el tiempo de duración de las simulaciones. Aun así, el desarrollo incremental realizado permitió optimizar el algoritmo, llevando el tiempo de ejección de 16 horas a 8 horas, y finalmente a 3 horas para llegar a un resultado aceptable.

El otro problema presentado fue el que se aprecia en la animación central de la Animación 1. Se observa la aparición de manchas en la imagen. El problema fue debido a un bug simple, el cual para la tercera prueba ya estaba solucionado.