Index of /~agv/elo320/01and02/tareas/soluciones/tarea3_1s02/ericnico03

1. Introducción

El Algoritmo de Dijkstra resuelve la ruta mas corta del nodo de origen al nodo de destino pasando por varias rutas de diferente costo, un ejmplo pudiera ser el siguiente: Descubrir la ruta la mas corta que debe recorrer el cartero sin hacerse  morder por los perros, en este caso el costo esta dado a la cantidad de perros en cada calle.
En la realidad el algoritmo de Dijkstra se usa con bastante frecuencia en protocolos de Enruteamento, considerando como costo el retraso u otros factores. Igualmente el Algoritmo de Dijkstra es de gran ayuda en operaciones de logística.
En este programa se toma un archivo texto el cual tiene un grafo que representa  la conectividad de los nodos con sus pesos respectivos en columnas, a dicho archivo se calcula Dijkstra. (Ruta mas corta del nodo destino a cada uno de los nodos dentro del grafo)






2.  Procedimiento

Es importante mencionar los supestos de la tarea:


• Los costos (o pesos) de las rutas son números positivos dentro del intervalo abierto ]0,1 [
• El Grafo ingresado es conexo
• Los números de los nodos son corelativos (no son saltados)

El programa funciona correctamente con cualquier grafo que cumpla con las especificaciones de la tarea, por motivos prácticos este Readme toma como ejemplo el Grafo entregado junto con la tarea:



0       1       0.41 1       2       0.51 2       3       0.50 4       3       0.36 3       5       0.38 3       0       0.45 0       5       0.29 5       4       0.21 1       4       0.32 4       2       0.32 5       1       0.29


El cual Gráficamente es representado de la siguiente manera:








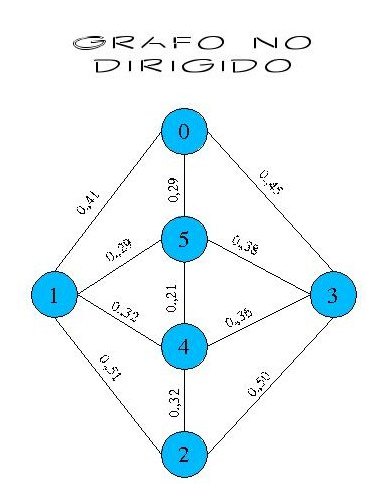
Existen dos posibilidades de implementación antes de Usar Dijkstra:


• Lista de Adyacencia:


Ver el siguiente gráfico:







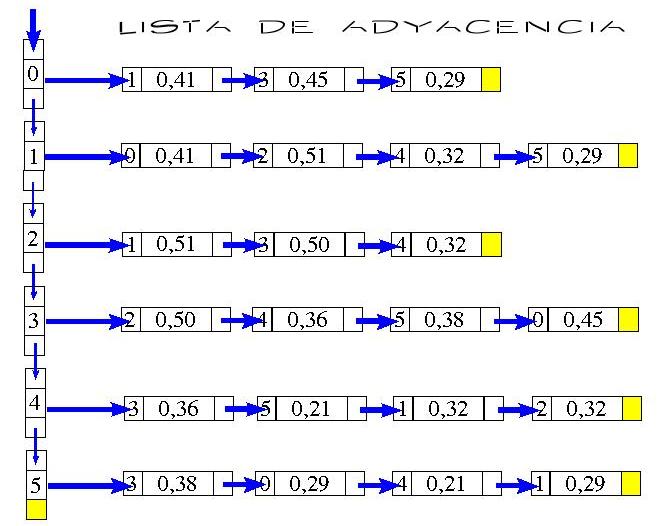
El uso de lista de adyacencia es de manera dinámica, al momento de insertar se usa un puntero llamado COLA el cual indica el último número Ingresado, de modo que al ingresar un nuevo nodo en la lista se compara con el Valor de COLA evitando la necesidad de recorrer toda la lista.
Para esta implementación se requiere un fuerte uso de punteros, por experiencia sabemos que el uso complejo de punteros y doble punteros pueden  producir Segmentation  Violetion por lo cual utilizamos la siguiente implementación:



• Matriz Adyacente:


El único defecto de esta implementación es que se debe conocer el tamaño de la matriz, el colocar un tamaño fijo es considerado como un gran error de programación (Cantidad de Nodos limitados y espacio en memoria desperdiciado) Por suerte la  entrada es un archivo, del cual podemos asignar facilmente el tamaño de la Matriz de manera dinámica, buscando la cantidad de nodos dentro del Archivo, (el cual cumple con los requisitos de la tarea). Para el uso de Matriz de Adyacencia basta con aplicar simples arreglos bidemensionales.

Obteniendo,  para este ejemplo, la siguiente Matriz de Adyacencia:



	0	1	2	3	4	5
0	-1	0.41	-1	0.45	-1	0.29
1	0.41	-1	0.51	-1	0.32	0.29
2	-1	0.51	-1	0.50	0.32	-1
3	0.45	-1	0.50	-1	0.36	0.38
4	0.32	0.32	-1	0.36	-1	0.21
5	0.29	0.29	-1	0.38	0.21	-1

Nota: Esta Matriz muestra el Costo entre un par de nodos, cuando el costo es igual a -1 significa que es el mismo nodo o de que no hay conectividad entre el par de nodos.
Al finalizar el programa se destruye esta matriz para liberar espacio en memoria.


3.  Instrucciones

Este Programa, ademas de cumplir con los requisitos de la tarea, incluye unos extras, por ejemplo,
a parte de ingresar como argumento de linea de comando  el nombre del archivo que incluye el Grafo, se puede ingresar opcionalmente el nodo de origen. (Por defecto el nodo de origen es el Cero)
Para ejecutar el Programa basta con Ingresar los siguientes instrucciones en la linea de comando (representado por #) :

# make

# ./dijkstra graph.txt 5


Donde:

• graph.txt es el archivo que contiene el grafo

• 5 es el nodo de origen

Nota: El programa es fuertemente robusto en el caso de que se ingrsen mal los Argumentos.

Para limpiar archivos *.o y ejecutable basta con colocar la siguiente sentencia:

# make clean

Otro Extra en este programa, a parte de indicar el nodo y la distancia, entrega como resultado el número de Saltos y la ruta por tomar (adicionalemente se muestra la Matriz Adyacente).

Un ejemplo del resultado de este programa es el Siguiente:

Origen : 5 ; Destino : 2

Número de saltos: 2

Métrica: 0.5300

Ruta   : 5 - 4 - 2