Diseño
y Programación Orientados a Objetos
1er. Sem 2016
Tarea 1: Bolas Libres y Enlazadas en Espacio Cerrado como Objetos de
Software
Lea detenidamente la tarea. Si algo no lo entiende, consulte en clases.
Si es preciso, se incorporarán aclaraciones al final.
Esta tarea tiene por objetivos:
* Ejercitar la configuración de un ambiente de trabajo para desarrollar
aplicaciones en lenguaje Java (se ha sugerido trabajar con Jgrasp o Eclipse )
* Modelar objetos reales como objetos de software.
* Reconocer clases y relaciones entre ellas en códigos fuentes Java.
* Ejercitar la extensión de clases dadas para satisfacer nuevos
requerimientos.
* Ejercitar la entrada y salida de datos.
* Conocer el formato .csv y su importación a planillas electrónicas.
* Ejercitar la preparación y entrega de resultados de software
(creación de makefiles, readme, documentación, manejo de repositorio
-GIT).
* Aprender una estrategia para programar simulaciones de fenómenos
continuos.
* Familiarización con una metodología de desarrollo "iterativa" e
"incremental".
Descripción General
En esta tarea se modela la interacción de objetos reales bolas,
resortes y
paredes sujetos a las leyes de la "naturaleza". A partir de
estos modelos se construyen clases para crear objetos de
software que representarán a los objetos reales. En física usted
estudió colisiones elásticas (conservación de energía además del
momentum) además la interacción de masas y resortes. Para calcular su
dinámica, en esta tarea las bolas
serán modeladas como esferas sin roce con la superficie y sin momento
angular. Decimos que éste es un modelo y no la realidad por todas
nuestras suposiciones; ejemplo de ello es la ausencia de roce con lo
cual las bolas no rodarán. Estas
suposiciones simplifican el modelo y permiten obtener resultados con
precisión satisfactoria.
Además tendremos recintos rectangulares cerrados fijos. Los resortes serán modelados sin masa y
cumplirán la ley
de Hooke
sin límite de elasticidad, es decir, Hooke vale en todas las
extensiones del resorte. Para determinar la dinámica de bolas sujetas a
fuerzas externas, revise este
material y éste (y Elastic Collision en wikipedia) para los choques elásticos.
Una vez que las clases básicas estén definidas, usted creará
instancias de bolas (Ball), resortes (Spring), y recintos cerrados
(Container). Luego objetos de software se pueden vincular a gusto para
representar a los sistemas reales que se desea simular. Notar que aquí
aparece otro actor: un simulador.
Una vez que las clases básicas estén definidas, usted creará
instancias de bolas y paredes en el modelo del mundo que estamos
describiendo para formar
un experimento a simular. Notar que aquí aparece otro actor:
un
simulador. El simulador no es más que el modelo del paso del tiempo, el
cual será informado a cada objeto. El tiempo avanzará en pasos
discretos en lugar de un continuo y así iremos avanzando en nuestra
simulación de a pasos
"pequeños" (deltas de tiempo). Un simulador no es más que el modelo del
paso del tiempo, el simulador informará el paso del tiempo a cada
objeto del sistema físico. El tiempo avanzará en pasos discretos en
lugar de un continuo y así iremos avanzando en nuestra simulación de a
pasos "pequeños" (deltas de tiempo).
Esta tarea les pide construir configuraciones de bolas, resortes
y recintos donde las bolas están confinadas en un espacio de dos
dimensiones,
todo en R2. Un ejemplo de tales escenarios se muestra en la
Figura 4.
Para ello usted contará con una solución bastante avanzada del problema
en R. Una vez que la configuración esté armada se inicia la
simulación por un tiempo definido por consola. Los resultados,
es decir las posiciones de los cuerpos en el tiempo, serán escritas en
pantalla.
Luego usted debe importar sus datos en una planilla electrónica para
generar gráficos del movimiento de sus objetos.
Desarrollo en Etapas
Para llegar al resultado final usted aplicará una metodología
"Iterativa e Incremental" para el desarrollo de software. Su grupo irá
desarrollando etapas que irán abordando los requerimientos
gradualmente. En cada etapa usted obtendrá una solución que funciona
para
un subconjunto de los requerimientos finales. Su grupo deberá entregar
una solución para cada una de las etapas aún cuando la última integre
las primeras. Esto tiene por finalidad, educar en la metodología iterativa e incremental.
Primera Etapa
Esta etapa busca simular choques entre dos bolas en R2 en espacio libre (sin contenedor).
Su grupo debe completar el código adjunto y modificar PhysicsLab1.java
proporcionado para reflejar la configuración de la Figura 1. Estudie
con detención la clase MyWorld, en particular el método simulate.
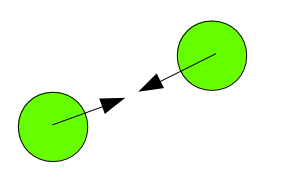
Figura 1: Dos bolas cochando en espacio libre
Segunda Etapa
Esta etapa amplía el requerimiento previo considerando choques entre bolas y con las paredes del contenedor en R2.
Su grupo debe crear la clase Contenedor y modificar
PhysicsLab2.java para reflejar la configuración de la
Figura 2.
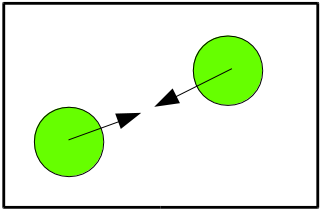
Figura 2: Dos bolas que se enfrentan directamente y chocan en ángulo en un recinto cerrado
Tercera Etapa
Como tercer paso usted completará el código previo para simular la
interacción entre dos bolas enlazadas con un resorte como se muestra en
Figura 3. Incluya el archivo PhysicsLab3.java que simule esta
canfiguración.
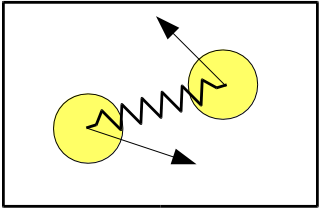
Figura 3: Dos bolas ligadas por un resorte en un recinto cerrado
Cuarta Etapa
Modifique la clase Ball para permitir enlaces de una bola con dos o más
bolas como se muestra en figura 4. Entregue archivo PhysicsLab4.java
para simular esta configuración.
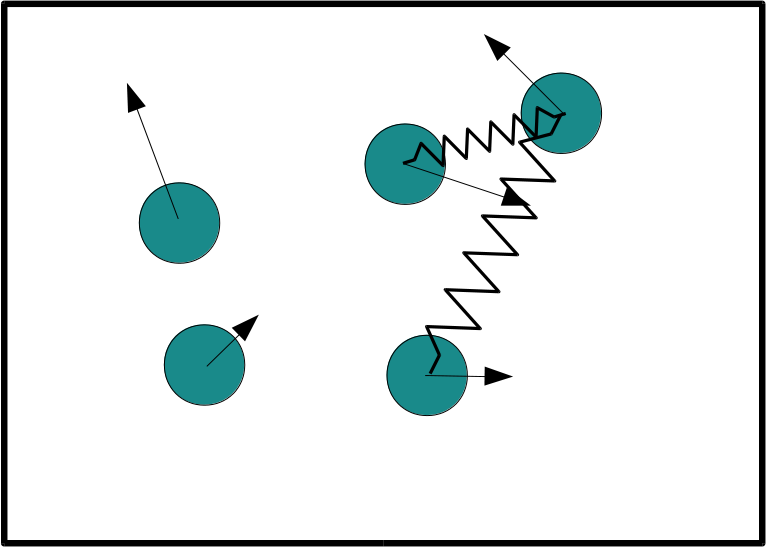
Figura 4: Configuración posible con bolas enlazadas y libres chocando en espacio cerrado en R
2
Resultados Esperados de su Grupo
Si
bien usted puede usar un IDE (Integrated Development Environment),
usted debe saber cómo compilar y correr su tarea desde la línea de
comandos.
Su tarea debe ser ejecutable en aragorn.elo.utfsm.cl usando:
$ java PhysicsLab <delta tiempo> <tiempo total a
simular> <periodo de muestreo>
La salida del programa será a pantalla.
Para efectos de esta tarea, el estado de salida sólo incluye las
posiciones de cada objeto.
El programa corre hasta generar toda la salida indicada. En
pantalla debería generar algo del tipo (caso figura 2):
Time,
Ball_0: x,y , Ball_1: x,y ,
Container_0: a0,b0,a1,b1
0.0, 1.0, 1.0 , 3.0 , 3.0, 0.0 , 0.0 ,
5.0, 4.0
/* aquí omito el resto de las líneas */
Usted deberá entregar los siguientes archivos:
- readme
- makefile /* para compilar */
- Archivo de
Documentación: para cada etapa, éste incluye la figura con la
configuración y un gráfico con curvas para la posición de las bolas
como función del tiempo
(x,t). Grafique t hasta que haya pasado la colisión en etapa 1, la
colisión con bola y pared en etapa 2, dos colisiones en etapa 3
cualquieran sean éstas, y 3 colisiones en etapa 4. Indique las
dificultades
encontradas y cómo las resolvió. Si usted desea analizar otro caso,
puede incluirlo.
- En directorios separados ponga los archivos de cada etapa.
- Se pide incluir los siguientes constructores como válidos para las clases señaladas:
public Vector2D(double x, doubble y)
public Ball(float mass, float radio, Vector2D position,
Vector2D speed, MyWorld world)
public Container(Vector2D upLeftPosition, Vector2D downRightPosition, MyWorld
world)
public Spring(float restLength, float stiffness)
La idea de definir estos constructores es que el ayudante
pueda
construir su configuración propia (PhysicsLab.java) y usar su implementación para generar
otros resultados.
Obviamente su programa no generará la figura de la configuración ni el gráfico. Puede usar
el dibujo aquí incluido y el gráfico lo debe generar con una planilla
de cálculo a partir de los datos de salida de su programa.
Extra créditos
Su grupo puede aspirar a 8 puntos adicionales (la nota
igualmente se satura en 100%) si incluye en la simulación gravedad y
roce. La gravedad la supondremos constante y el roce será una fuerza
disipativa (roce de
fluido)
que supondremos proporcional a la magnitud de la velocidad y el radio
de cada bola. En archivo Readme indique si abordó
este requerimiento. La constante de proporcionalidad del roce y la
gravedad en este caso son pasados como parámetros opcionales al ejecutar la simulación.
Ayudas
* Revise las instrucciones parra la realización de tareas.
* Dé una mirada a los códigos de avance proporcionados. Si encuentra errores o algo mejorable, avise al profesor.
* Para enviar los datos a un archivo de salida, redireccione la salida
a pantalla usando:
$ java PhysicsLab 0.01 15 0.1 > miSalida.csv
Luego trate este archivo como si fuera planilla electrónica. Usted
podrá usar las "comas" y "tabs" como separadores de columnas.
* No dude en consultar al profesor o ayudante sobre dudas de esta tarea.
* La
fuerza de fricción con el aire depende el aire y forma del cuerpo.
Quienes opten por los créditos adicionaeles pueden modelar esta fuerza
como proporcional a la velocidad del cuerpo
(es una aproximación válida cuando no hay turbulencias -caso
velocidades bajas). La constante de proporcionalidad la podemos modelar
de dos formas: como constante para todas las masas, o como el producto
de la viscosidad del aire por un factor que depende de la geometría de
cada cuerpo. Si usamos el primer enfoque, la Constante de Roce Viscoso
(viscous friction constant) , será un atributo más de MyWorld (similar
a g). Si usamos el segundo enfoque, podemos asociar la viscosidad del
aire a MyWorld y una constante "crossSection" (sección eficaz) a
cada masa. La Constante de Roce Viscoso en este último caso será el
producto de ambas.
* En myphysicslab.com usted
podrá encontrar otras simulaciones hechas en Java. El método usado en
este caso difiere del usado aquí. El nuestro es más flexible.
Nociones de simulación de fenómenos
continuos
La idea básica usada en esta tarea es discretizar el tiempo; para cada
instante discreto, congelamos el tiempo y pedimos a cada objeto
del experimento calcular cuál será su estado futuro (delta t más tarde)
a partir del estado actual y las condiciones en que está sometido. Es
importante congelar el tiempo y hacer este cálculo para cada objeto.
Luego pedimos a todos actualizar su estado basado en lo calculado y
avanzamos el tiempo en ese delta. Esta simple idea trabaja bien aquí y en muchas situaciones, pero no en
todas; por ejemplo si deseáramos permitir que dos resortes estén
juntos uno después del otro. En estos casos, como aproximación podemos usar
una masa pequeña entre ambos. Si quisiéramos pegar dos bolas juntas, podemos
poner un resorte muy pequeño entre ambos con constante elástica "infinita".
Lo mismo si deseamos modelar barras rígidas. Para los casos de resortes de
constante elástica muy grandes, la calidad de la simulación baja si no
usamos un delta_t lo suficientemente pequeño (la simulación tomará tiempo de
ejecución).
Una vez hecha la tares, usted debería notar que es posible incorporar
gravedad y pensar que el plano R2 es vertical (caso extra ccréditos). Cuerdas pueden ser modeladas como resortes con constante
elástica "infinita" cuando se extiende respecto al reposo y cero cuando se
acorta respecto a su largo de reposo.
Se
puede jugar cambiando los tamaños o el número de bolas involucradas.
Cuando hay muchas bolas, se podría estimar la presión lineal (fuerza
por unidad de longitud) en las paredes. Al analizar todo verticalmente
se debería poder apreciar una mayor concentración de bolas en promedio
en las partes bajas. Por otro lado, este ramo no es el único
donde deben rendir bien este semestre. No entusiasmarse mucho.




